| 根軌跡和系統(tǒng)參數(shù)的確定 | 您所在的位置:網(wǎng)站首頁(yè) › 屬鼠2021年佩戴什么 › 根軌跡和系統(tǒng)參數(shù)的確定 |
根軌跡和系統(tǒng)參數(shù)的確定
|
文章目錄
1、根軌跡2、根軌跡定義3、根軌跡的繪制4、根軌跡的作用
1、根軌跡
前面有講到通過(guò)閉環(huán)傳遞函數(shù)的極點(diǎn)分布情況來(lái)判斷系統(tǒng)是否穩(wěn)定。當(dāng)然還有些更簡(jiǎn)單的判別方式,例如:勞斯穩(wěn)定性判據(jù)、赫爾維茨穩(wěn)定性判據(jù)等。但都是判斷系統(tǒng)是否穩(wěn)定的,那么怎么判斷系統(tǒng)的穩(wěn)定程度(穩(wěn)定裕度)呢?或者說(shuō)當(dāng)一個(gè)系統(tǒng)參數(shù)在什么范圍內(nèi)系統(tǒng)穩(wěn)定,取多大時(shí)穩(wěn)定裕度最好。 舉個(gè)例子: 因此有個(gè)工程師發(fā)明了一套技巧,不需要每一個(gè)具體的K反復(fù)求閉環(huán)特征根,只需通過(guò)開(kāi)環(huán)傳遞函數(shù)Gk(s)的零極點(diǎn)就能得到當(dāng)開(kāi)環(huán)增益 K → ∞ K\rightarrow \infty K→∞ 時(shí),閉環(huán)系統(tǒng)的特征根在復(fù)平面上的變化軌跡。 這就是常規(guī)根軌跡法。 2、根軌跡定義根軌跡是開(kāi)環(huán)系統(tǒng)某一參數(shù)從零變到無(wú)窮時(shí),閉環(huán)系統(tǒng)特征方程式的根在s平面上變化的軌跡 3、根軌跡的繪制只需要利用開(kāi)環(huán)零極點(diǎn),就能繪制常規(guī)根軌跡。(根據(jù)開(kāi)環(huán)零極點(diǎn),描繪閉環(huán)特征根(極點(diǎn))的曲線) 看下上面的例子用常規(guī)根軌跡法,只需要依靠開(kāi)環(huán)零極點(diǎn): 下面用matlab繪制上面閉環(huán)系統(tǒng)的根軌跡。
在分析系統(tǒng)性能的時(shí)候,除了某一根軌跡點(diǎn)對(duì)應(yīng)的開(kāi)環(huán)增益外,有時(shí)還需要知道該增益所對(duì)應(yīng)的其他閉環(huán)極點(diǎn)的值,這時(shí)候則只需輸入以下命令即可:[K,p]=rlocfind(sys);然后繪圖上出現(xiàn)十字光標(biāo),只要點(diǎn)擊根軌跡上的一點(diǎn),命令窗口就會(huì)顯示出,當(dāng)前增益K的值,和其他的極點(diǎn)。 程序如下: >> num=[1]; %開(kāi)環(huán)傳函分子多項(xiàng)式系數(shù) den=conv([1,1,0],[1,2]); %開(kāi)環(huán)傳函分母多項(xiàng)式系數(shù) sys=tf(num,den); %系統(tǒng)傳遞函數(shù)模型 rlocus(sys) %繪制系統(tǒng)的根軌跡圖 [K,p]=rlocfind(sys) 4、根軌跡的作用1. 從根軌跡的分布直觀來(lái)說(shuō)可以看出當(dāng)K增加至多大時(shí),系統(tǒng)會(huì)不穩(wěn)定。 2. 根軌跡離虛軸越遠(yuǎn),那么系統(tǒng)就越不容易因?yàn)樽陨韰?shù)K的變化而失去穩(wěn)定,則系統(tǒng)的穩(wěn)定程度就越高。 3. 如果系統(tǒng)的穩(wěn)定程度不足的話,還可以在開(kāi)環(huán)傳遞函數(shù)中增加零點(diǎn),使得根軌跡左移,增加系統(tǒng)的穩(wěn)定程度。這樣一來(lái),對(duì)系統(tǒng)穩(wěn)定裕度的校正就變的非常直觀了。 注意:根軌跡是S域(復(fù)頻域)設(shè)計(jì)法,是依靠S來(lái)解決問(wèn)題的。 那么K取值多少時(shí)系統(tǒng)比較穩(wěn)定呢? 借助根軌跡這一工具, 我們可以看出隨著系統(tǒng)參數(shù)變化,系統(tǒng)極點(diǎn)的分布情況,繼而判定系統(tǒng)的穩(wěn)定性及穩(wěn)定邊界。為獲得較好的動(dòng)穩(wěn)態(tài)性能,常常取阻尼 ξ \xi ξ=0.707 對(duì)應(yīng)的增益為最終的參數(shù)值。 首先利用matlab繪制出相應(yīng)的根軌跡圖: >> s=tf('s'); G=1/s/(s+1)/(s+2); figure; rlocus(G)結(jié)果如下圖: 當(dāng)K>6.03時(shí),系統(tǒng)存在右半平面極點(diǎn),系統(tǒng)不再穩(wěn)定,因此,K應(yīng)小于6.03。 當(dāng)K=0.655時(shí),系統(tǒng)阻尼約為0.705,系統(tǒng)的動(dòng)態(tài)性能較佳。 根據(jù)上述分析,開(kāi)環(huán)傳遞函數(shù)的最佳增益為0.655。利用step指令,可觀察不同K值下,系統(tǒng)的階躍響應(yīng)。 s=tf('s'); K=[0.2 0.655 1]; for n=1:3 G=K(n)/s/(s+1)/(s+2); Gc=feedback(G,1); step(Gc) hold on end
從圖中可以看出,K=0.655 確實(shí)在響應(yīng)時(shí)間、超調(diào)量及調(diào)節(jié)時(shí)間之間得到折中,證實(shí)了前述參數(shù)設(shè)計(jì)方法的正確性。 |
【本文地址】
 注意上面的閉環(huán)傳函為單位負(fù)反饋的。那么K的取值是什么范圍時(shí)該系統(tǒng)穩(wěn)定呢,當(dāng)然可以用勞斯判據(jù)求出。但K值取多少時(shí)最穩(wěn)定呢,這里就涉及到了根軌跡(系統(tǒng)特征根的軌跡)了。那么我們讓K的取值從0到正無(wú)窮時(shí),求出閉環(huán)傳函的特征方程的各個(gè)根,這樣就形成了根軌跡了。但是這樣做要做大量的運(yùn)算,很復(fù)雜耗時(shí)。
注意上面的閉環(huán)傳函為單位負(fù)反饋的。那么K的取值是什么范圍時(shí)該系統(tǒng)穩(wěn)定呢,當(dāng)然可以用勞斯判據(jù)求出。但K值取多少時(shí)最穩(wěn)定呢,這里就涉及到了根軌跡(系統(tǒng)特征根的軌跡)了。那么我們讓K的取值從0到正無(wú)窮時(shí),求出閉環(huán)傳函的特征方程的各個(gè)根,這樣就形成了根軌跡了。但是這樣做要做大量的運(yùn)算,很復(fù)雜耗時(shí)。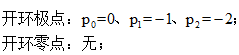 就能得到K從0變化的無(wú)窮大時(shí),根的軌跡大概的樣子(我們不介紹怎么具體畫(huà)根軌跡):
就能得到K從0變化的無(wú)窮大時(shí),根的軌跡大概的樣子(我們不介紹怎么具體畫(huà)根軌跡): 
 從上面可以看出系統(tǒng)的三個(gè)極點(diǎn),本例題中沒(méi)有零點(diǎn)。而且只有在K 滿足一定條件的情況下系統(tǒng)才是穩(wěn)定的。
從上面可以看出系統(tǒng)的三個(gè)極點(diǎn),本例題中沒(méi)有零點(diǎn)。而且只有在K 滿足一定條件的情況下系統(tǒng)才是穩(wěn)定的。 從圖中可以出:
從圖中可以出: