| 【圖神經(jīng)網(wǎng)絡(luò)】10分鐘掌握?qǐng)D神經(jīng)網(wǎng)絡(luò)及其經(jīng)典模型 | 您所在的位置:網(wǎng)站首頁(yè) › 屬馬的男生最佳配偶是什么屬相呢 › 【圖神經(jīng)網(wǎng)絡(luò)】10分鐘掌握?qǐng)D神經(jīng)網(wǎng)絡(luò)及其經(jīng)典模型 |
【圖神經(jīng)網(wǎng)絡(luò)】10分鐘掌握?qǐng)D神經(jīng)網(wǎng)絡(luò)及其經(jīng)典模型
|
10分鐘掌握?qǐng)D神經(jīng)網(wǎng)絡(luò)及其經(jīng)典模型
1. 圖的基本概念1.1 圖的表示
2. 圖神經(jīng)網(wǎng)絡(luò)的基本概念2.1 了解圖神經(jīng)網(wǎng)絡(luò)2.2 消息傳遞2.3 最后的向量表征有什么用?
3. 經(jīng)典的圖神經(jīng)網(wǎng)絡(luò)模型3.1 GCN: Graph Convolution Networks3.2 GraphSAGE:歸納式學(xué)習(xí)框架3.3 GAT:Attention機(jī)制
4. 流行的圖神經(jīng)網(wǎng)絡(luò)模型4.1 無(wú)監(jiān)督的節(jié)點(diǎn)表示學(xué)習(xí)(Unsupervised Node Representation)4.1.1 GAE: Graph Auto-Encoder
4.2 Graph Pooling4.2.1 DiffPool
5. 實(shí)現(xiàn)圖神經(jīng)網(wǎng)絡(luò)的步驟6. 推薦書籍參考資料
圖(Graph)是一種數(shù)據(jù)結(jié)構(gòu),能夠很自然地建模現(xiàn)實(shí)場(chǎng)景中一組實(shí)體之間的復(fù)雜關(guān)系。在真實(shí)世界中,很多數(shù)據(jù)往往以圖的形式出現(xiàn), 例如社交網(wǎng)絡(luò)、電商購(gòu)物、蛋白質(zhì)相互作用關(guān)系等。因此,近些年來(lái)使用智能化方式來(lái)建模分析圖結(jié)構(gòu)的研究越來(lái)越受到關(guān)注, 其中基于深度學(xué)習(xí)的圖建模方法的圖神經(jīng)網(wǎng)絡(luò)(Graph Neural Network, GNN), 因其出色的性能已廣泛應(yīng)用于社會(huì)科學(xué)、自然科學(xué)等多個(gè)領(lǐng)域。
圖可以表示很多事物——社交網(wǎng)絡(luò)、分子等等。節(jié)點(diǎn)可以表示用戶/產(chǎn)品/原子,而邊表示它們之間的連接,比如關(guān)注/通常與相連接的產(chǎn)品同時(shí)購(gòu)買/鍵。社交網(wǎng)絡(luò)圖可能看起來(lái)像是這樣,其中節(jié)點(diǎn)是用戶,邊則是連接: 通常使用 G = ( V , E ) G=(V, E) G=(V,E)來(lái)表示圖,其中 V V V表示節(jié)點(diǎn)的集合、 E E E表示邊的集合。對(duì)于兩個(gè)相鄰節(jié)點(diǎn) u , v u, v u,v, 使用 e = ( u , v ) e=(u,v) e=(u,v)表示這兩個(gè)節(jié)點(diǎn)之間的邊。兩個(gè)節(jié)點(diǎn)之間邊既可能是有向,也可能無(wú)向。若有向,則稱之有向圖(Directed Graph), 反之,稱之為無(wú)向圖(Undirected Graph)。 1.1 圖的表示在圖神經(jīng)網(wǎng)絡(luò)中,常見的表示方法有鄰接矩陣、度矩陣、拉普拉斯矩陣等。 鄰接矩陣(Adjacency Matrix) 用于表示圖中節(jié)點(diǎn)之間的關(guān)系,對(duì)于n個(gè)節(jié)點(diǎn)的簡(jiǎn)單圖,有鄰接矩陣 A ∈ R n × n A\in R^{n\times n} A∈Rn×n: A i j = { 1 ?if? ( v i , v j ) ∈ E and i ≠ j 0 ?else? A_{ij}=\begin{cases}1 & \text{ if } (v_i,v_j)\in E \text{and} i\ne j \\0 & \text{ else }\end{cases} Aij?={10??if?(vi?,vj?)∈Eandi=j?else?? 度矩陣(Degree Matrix) 節(jié)點(diǎn)的度(Degree)表示與該節(jié)點(diǎn)相連的邊的個(gè)數(shù),記作d(v)。對(duì)于n個(gè)節(jié)點(diǎn)的簡(jiǎn)單圖G=(V, E),其度矩陣D為 D i i = d ( v ) D_{ii}=d(v) Dii?=d(v),也是一個(gè)對(duì)角矩陣。 拉普拉斯矩陣 (Laplacian Matrix) 對(duì)于n個(gè)節(jié)點(diǎn)的簡(jiǎn)單圖 G = ( V , E ) G=(V, E) G=(V,E),其拉普拉斯矩陣定義為 L = D ? A L=D-A L=D?A,其中 D D D、 A A A為上面提到過的度矩陣和鄰接矩陣. 將其歸一化后有 L s y m = D ? 1 / 2 L D ? 1 / 2 L^{sym}=D^{-1/2}LD^{-1/2} Lsym=D?1/2LD?1/2。 2. 圖神經(jīng)網(wǎng)絡(luò)的基本概念 2.1 了解圖神經(jīng)網(wǎng)絡(luò)每個(gè)節(jié)點(diǎn)都有一組定義它的特征。在社交網(wǎng)絡(luò)圖的案例中,這些特征可以是年齡、性別、居住國(guó)家、政治傾向等。每條邊連接的節(jié)點(diǎn)都可能具有相似的特征。這體現(xiàn)了這些節(jié)點(diǎn)之間的某種相關(guān)性或關(guān)系。 假設(shè)我們有一個(gè)圖 G,其具有以下頂點(diǎn)和邊: 注意:在實(shí)際運(yùn)用中,盡量不要使用 one-hot 編碼,因?yàn)楣?jié)點(diǎn)的順序可能會(huì)非常混亂。相反,應(yīng)該使用可明顯區(qū)分節(jié)點(diǎn)的特征,比如對(duì)社交網(wǎng)絡(luò)而言,可選擇年齡、性別、政治傾向等特征;對(duì)分子研究而言可選擇可量化的化學(xué)性質(zhì)。 現(xiàn)在,我們有節(jié)點(diǎn)的 one-hot 編碼(或嵌入)了,接下來(lái)我們將神經(jīng)網(wǎng)絡(luò)引入這一混合信息中來(lái)實(shí)現(xiàn)對(duì)圖的修改。所有的節(jié)點(diǎn)都可轉(zhuǎn)化為循環(huán)單元(或其它任何神經(jīng)網(wǎng)絡(luò)架構(gòu),只是我這里使用的是循環(huán)單元);所有的邊都包含簡(jiǎn)單的前饋神經(jīng)網(wǎng)絡(luò)。那么看起來(lái)會(huì)是這樣: 一旦節(jié)點(diǎn)和邊的轉(zhuǎn)化完成,圖就可在節(jié)點(diǎn)之間執(zhí)行消息傳遞。這個(gè)過程也被稱為「近鄰聚合(Neighbourhood Aggregation)」,因?yàn)槠渖婕暗絿@給定節(jié)點(diǎn),通過有向邊從周圍節(jié)點(diǎn)推送消息(即嵌入)。 注意:有時(shí)候可為不同類型的邊使用不同的神經(jīng)網(wǎng)絡(luò),比如為單向邊使用一種神經(jīng)網(wǎng)絡(luò),為雙向邊使用另一種神經(jīng)網(wǎng)絡(luò)。這樣仍然可以獲取節(jié)點(diǎn)之間的空間關(guān)系。 就 GNN 而言,對(duì)于單個(gè)參考節(jié)點(diǎn),近鄰節(jié)點(diǎn)會(huì)通過邊神經(jīng)網(wǎng)絡(luò)向參考節(jié)點(diǎn)上的循環(huán)單元傳遞它們的消息(嵌入)。參考循環(huán)單位的新嵌入更新,基于在循環(huán)嵌入和近鄰節(jié)點(diǎn)嵌入的邊神經(jīng)網(wǎng)絡(luò)輸出的和上使用循環(huán)函數(shù)。我們把上面的紅色節(jié)點(diǎn)放大看看,并對(duì)這一過程進(jìn)行可視化: 這個(gè)過程是在網(wǎng)絡(luò)中的所有節(jié)點(diǎn)上并行執(zhí)行的,因?yàn)?L+1 層的嵌入取決于 L 層的嵌入。因此,在實(shí)踐中,我們并不需要從一個(gè)節(jié)點(diǎn)「移動(dòng)」到另一節(jié)點(diǎn)就能執(zhí)行消息傳遞。 注意:邊神經(jīng)網(wǎng)絡(luò)輸出(黑色信封)之和與輸出的順序無(wú)關(guān)。 正式地,圖神經(jīng)網(wǎng)絡(luò)(GNN)最早由Marco Gori、Franco Scarselli等人提出,他們將神經(jīng)網(wǎng)絡(luò)方法拓展到了圖數(shù)據(jù)計(jì)算領(lǐng)域。在Scarselli論文中典型的圖如圖1所示: 為了根據(jù)輸入節(jié)點(diǎn)鄰居信息更新節(jié)點(diǎn)狀態(tài),將局部轉(zhuǎn)移函數(shù) f f f定義為循環(huán)遞歸函數(shù)的形式, 每個(gè)節(jié)點(diǎn)以周圍鄰居節(jié)點(diǎn)和相連的邊作為來(lái)源信息來(lái)更新自身的表達(dá) h h h。為了得到節(jié)點(diǎn)的輸出 o o o, 引入局部輸出函數(shù) g g g。因此,有以下定義: h n = f ( x n , x c o [ n ] , x n e [ n ] , h n e [ n ] ) ( 1 ) h_n=f(x_n, x_{co[n]}, x_{ne[n]}, h_{ne[n]}) \quad (1) hn?=f(xn?,xco[n]?,xne[n]?,hne[n]?)(1) o n = g ( h n , x n ) ( 2 ) o_n=g(h_n, x_n) \quad (2) on?=g(hn?,xn?)(2) 其中 x x x表示當(dāng)前節(jié)點(diǎn), h h h表示節(jié)點(diǎn)隱狀態(tài), n e [ n ] ne[n] ne[n]表示表示節(jié)點(diǎn)n的鄰居節(jié)點(diǎn)集合, c o [ n ] co[n] co[n]表示節(jié)點(diǎn)n的鄰接邊的集合。以圖1的L1節(jié)點(diǎn)為例, X 1 X1 X1是其輸入特征, n e [ l 1 ] ne[l_1] ne[l1?]包含節(jié)點(diǎn) l 2 , l 3 , l 4 , l 6 l_2, l_3, l_4, l_6 l2?,l3?,l4?,l6?, c o [ l 1 ] co[l_1] co[l1?]包含邊 l ( 3 , 1 ) , l ( 1 , 4 ) , l ( 6 , 1 ) , l ( 1 , 2 ) l_{(3,1)}, l_{(1,4)}, l_{(6,1)}, l_{(1,2)} l(3,1)?,l(1,4)?,l(6,1)?,l(1,2)?。 將所有局部轉(zhuǎn)移函數(shù) f f f堆疊起來(lái), 有: H = F ( H , X ) ( 3 ) H=F(H,X) \quad (3) H=F(H,X)(3) O = G ( H , X n ) ( 4 ) O=G(H,X_n) \quad (4) O=G(H,Xn?)(4)其中F是全局轉(zhuǎn)移函數(shù)(Global Transition Function), G是全局輸出函數(shù)(Global Output Function)。 根據(jù)巴拿赫不動(dòng)點(diǎn)定理,假設(shè)公式(3)的F是壓縮映射,那么不動(dòng)點(diǎn)H的值就可以唯一確定,根據(jù)以下方式迭代求解: H t + 1 = F ( H t , X ) ( 5 ) H^{t+1}=F(H^t, X) \quad (5) Ht+1=F(Ht,X)(5)基于不動(dòng)點(diǎn)定理,對(duì)于任意初始值,GNN會(huì)按照公式(5)收斂到公式(3)描述的解。 2.3 最后的向量表征有什么用?執(zhí)行了幾次近鄰聚合/消息傳遞流程之后,每個(gè)節(jié)點(diǎn)的循環(huán)單元都會(huì)獲得一組全新的嵌入。此外,經(jīng)過多個(gè)時(shí)間步驟/多輪消息傳遞之后,節(jié)點(diǎn)對(duì)自己和近鄰節(jié)點(diǎn)的信息(特征)也會(huì)有更好的了解。這會(huì)為整個(gè)圖創(chuàng)建出更加準(zhǔn)確的表征。 要進(jìn)一步在該流程的更高層面上進(jìn)行處理或者只是簡(jiǎn)單地表征該圖,你可以將所有嵌入加到一起得到向量 H 來(lái)表示整個(gè)圖。使用 H 比使用鄰接矩陣更好,因?yàn)椴还茉鯓訉?duì)圖進(jìn)行扭轉(zhuǎn)變形,這些矩陣都并不表征圖的特征或獨(dú)特性質(zhì)——只是節(jié)點(diǎn)之間的邊連接(這在某些情形下并不是很重要)。 總結(jié)一下,將所有節(jié)點(diǎn)循環(huán)單元的最終向量表征加到一起(當(dāng)然,與順序無(wú)關(guān)),然后使用所得到的向量作為其它工作過程的輸入或簡(jiǎn)單地將其用于表征該圖。這個(gè)步驟看起來(lái)如下圖所示: GCN可謂是圖神經(jīng)網(wǎng)絡(luò)的“開山之作”,它首次將圖像處理中的卷積作簡(jiǎn)單的用到圖結(jié)構(gòu)數(shù)據(jù)處理中來(lái),并且給出了具體的推導(dǎo),這里面涉及到復(fù)雜的譜圖理論。2017年,Thomas N. Kipf等人提出GCN模型. 其結(jié)構(gòu)如圖2所示: 假設(shè)需要構(gòu)造一個(gè)兩層的GCN,激活函數(shù)分別采用ReLU和Softmax,則整體的正向傳播的公式如下所示: Z = f ( X , A ) = s o f t m a x ( A ^ ReLU ( A ^ X W ( 0 ) ) W ( 1 ) ) ( 6 ) Z=f(X,A)=softmax(\hat{A} \text{ReLU}(\hat{A}XW^{(0)})W^{(1)}) \quad (6) Z=f(X,A)=softmax(A^ReLU(A^XW(0))W(1))(6) A ^ = D ~ ? 1 2 A ~ D ~ ? 1 2 ( 7 ) \hat{A}=\tilde {D}^{-\frac{1}{2}} \tilde{A}\tilde {D}^{-\frac{1}{2}} \quad (7) A^=D~?21?A~D~?21?(7) 其中 W ( 0 ) W^{(0)} W(0)表示第一層的權(quán)重矩陣, W ( 1 ) W^{(1)} W(1)表示第二層的權(quán)重矩陣,X為節(jié)點(diǎn)特征, A ~ \tilde{A} A~等于鄰接矩陣A和單位矩陣相加,\tilde{D}為 A A A的度矩陣。 從上面的正向傳播公式和示意圖來(lái)看,GCN好像跟基礎(chǔ)GNN沒什么區(qū)別。接下里給出GCN的傳遞公式(8):
H
(
l
+
1
)
=
σ
(
D
~
?
1
2
A
~
D
~
?
1
2
H
(
l
)
W
(
l
)
)
(
8
)
H^{(l+1)}=\sigma (\tilde {D}^{-\frac{1}{2}}\tilde {A}\tilde {D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) \quad (8)
H(l+1)=σ(D~?21?A~D~?21?H(l)W(l))(8) 觀察一下歸一化的矩陣與特征向量矩陣的乘積: 一個(gè)graph attention layer的結(jié)構(gòu)如圖4所示,節(jié)點(diǎn)
i
,
j
i,j
i,j的特征作為輸出,計(jì)算兩節(jié)點(diǎn)之間的注意力權(quán)重。 同樣是在每個(gè)節(jié)點(diǎn)間共享self-attention機(jī)制: a : R F ′ × R F ′ → R a:\mathbb{R}^{F'}\times \mathbb{R}^{F'}\rightarrow \mathbb{R} a:RF′×RF′→R,可計(jì)算節(jié)點(diǎn) i i i和 j j j之間的attention 系數(shù)如下: e i j = a ( W h ? i , W h ? j ) e_{ij}=a(W\vec{h}_i, W\vec{h}_j) eij?=a(Wh i?,Wh j?)該系數(shù)表示了節(jié)點(diǎn) i i i的特征對(duì)節(jié)點(diǎn) j j j的重要性。注意機(jī)制 a ( ? ) a(\cdot) a(?)是一個(gè)單層前饋神經(jīng)網(wǎng)絡(luò),用一個(gè)權(quán)重向量來(lái)表示: a ? ∈ R 2 F ′ \vec{a}\in \mathbb{R}^{2F'} a ∈R2F′,它把拼接后的長(zhǎng)度為 2 F 2F 2F的高維特征映射到一個(gè)實(shí)數(shù)上,作為注意力系數(shù)。 attention 機(jī)制分為以下兩種: Global graph attention:允許每個(gè)節(jié)點(diǎn)參與其他任意節(jié)點(diǎn)的注意力機(jī)制,它忽略了所有的圖結(jié)構(gòu)信息。Masked graph attention:只允許鄰接節(jié)點(diǎn)參與當(dāng)前節(jié)點(diǎn)的注意力機(jī)制中,進(jìn)而引入了圖的結(jié)構(gòu)信息。論文種采用Masked graph attention,并且鄰接節(jié)點(diǎn)是一階鄰接節(jié)點(diǎn)(包括節(jié)點(diǎn)本身)。 為了穩(wěn)定self-attention的學(xué)習(xí)過程,GAT原文使用多頭注意力機(jī)制(Multi-head attention)。具體地,使
K
K
K個(gè)獨(dú)立注意力機(jī)制根據(jù)上式進(jìn)行變換,得到更新的節(jié)點(diǎn)輸出特征,然后將
K
K
K個(gè)特征拼接(concat),得到如下輸出特征: 總結(jié)一下,GAT的一些優(yōu)點(diǎn): (1)訓(xùn)練GCN無(wú)需了解整個(gè)圖結(jié)構(gòu),只需知道每個(gè)節(jié)點(diǎn)的鄰居節(jié)點(diǎn)即可; (2)計(jì)算速度快,可以在不同的節(jié)點(diǎn)上進(jìn)行并行計(jì)算; (3)既可以用于Transductive Learning,又可以用于Inductive Learning,可以對(duì)未見過的圖結(jié)構(gòu)進(jìn)行處理。 4. 流行的圖神經(jīng)網(wǎng)絡(luò)模型 4.1 無(wú)監(jiān)督的節(jié)點(diǎn)表示學(xué)習(xí)(Unsupervised Node Representation)由于標(biāo)注數(shù)據(jù)的成本非常高,如果能夠利用無(wú)監(jiān)督的方法很好的學(xué)習(xí)到節(jié)點(diǎn)的表示,將會(huì)有巨大的價(jià)值和意義,例如找到相同興趣的社區(qū)、發(fā)現(xiàn)大規(guī)模的圖中有趣的結(jié)構(gòu)等等。 在介紹Graph Auto-Encoder之前,需要先了解自編碼器(Auto-Encoder)、變分自編碼器(Variational Auto-Encoder),這里就不贅述。理解了自編碼器之后,再來(lái)理解變分圖的自編碼器就容易多了。如下圖所示,輸入圖的鄰接矩陣A 和節(jié)點(diǎn)的特征矩陣X,通過編碼器(圖卷積網(wǎng)絡(luò))學(xué)習(xí)節(jié)點(diǎn)低維向量表示的均值
μ
\mu
μ和方差
σ
\sigma
σ,然后用解碼器(鏈路預(yù)測(cè))生成圖。 Graph pooling是GNN中很流行的一種作,目的是為了獲取一整個(gè)圖的表示,主要用于處理圖級(jí)別的分類任務(wù),例如在有監(jiān)督的圖分類、文檔分類等等。 在圖級(jí)別的任務(wù)當(dāng)中,當(dāng)前的很多方法是將所有的節(jié)點(diǎn)嵌入進(jìn)行全局池化,忽略了圖中可能存在的任何層級(jí)結(jié)構(gòu),這對(duì)于圖的分類任務(wù)來(lái)說(shuō)尤其成問題,因?yàn)槠淠繕?biāo)是預(yù)測(cè)整個(gè)圖的標(biāo)簽。針對(duì)這個(gè)問題,斯坦福大學(xué)團(tuán)隊(duì)提出了一個(gè)用于圖分類的可微池化作模塊——DiffPool,可以生成圖的層級(jí)表示,并且可以以端到端的方式被各種圖神經(jīng)網(wǎng)絡(luò)整合。 DiffPool的核心思想是通過一個(gè)可微池化作模塊去分層地聚合圖節(jié)點(diǎn),具體的,這個(gè)可微池化作模塊基于GNN上一層生成的節(jié)點(diǎn)嵌入X以及分配矩陣S ,以端到端的方式分配給下一層的簇,然后將這些簇輸入到GNN下一層,進(jìn)而實(shí)現(xiàn)用分層的方式堆疊多個(gè)GNN層的想法。 具體地,給定一個(gè)GNN模塊的輸出 Z = GNN ( A , X ) Z=\text{GNN}(A,X) Z=GNN(A,X)和一個(gè)圖的鄰接矩陣 A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n,目標(biāo)是尋找一種方式可以得到一個(gè)新的包含 m < n m n_{l+1} nl?>nl+1?,即行數(shù)等于第 l l l層的節(jié)點(diǎn)數(shù)(cluster數(shù)),列數(shù)代表第 l + 1 l+1 l+1層的節(jié)點(diǎn)數(shù)(cluster數(shù))。assignment matrix表示第 l l l層的每一個(gè)節(jié)點(diǎn)到第 l + 1 l+1 l+1層的每一個(gè)節(jié)點(diǎn)(或cluster)的概率。 假設(shè) S ( l ) S^{(l)} S(l)是預(yù)先計(jì)算好的。DIFFPOOL層 ( A ( l + 1 ) , X ( l + 1 ) ) = DIFFPOOL ? ( A ( l ) , Z ( l ) ) \left(A^{(l+1)}, X^{(l+1)}\right)=\operatorname{DIFFPOOL}\left(A^{(l)}, Z^{(l)}\right) (A(l+1),X(l+1))=DIFFPOOL(A(l),Z(l))表示粗化輸入圖,然后生成一個(gè)新的鄰接矩陣 A ( l + 1 ) A^{(l+1)} A(l+1)和新的embeddings矩陣 X ( l + 1 ) X^{(l+1)} X(l+1): X ( l + 1 ) = S ( l ) T Z ( l ) ∈ R n l + 1 × d X^{(l+1)}=S^{(l)^{T}} Z^{(l)} \in \mathbb{R}^{n_{l+1} \times d} X(l+1)=S(l)TZ(l)∈Rnl+1?×d X i ( l + 1 ) X_i^{(l+1)} Xi(l+1)?表示第 l + 1 l+1 l+1層cluster i i i的embedding A ( l + 1 ) = S ( l ) T A ( l ) S ( l ) ∈ R n l + 1 × n l + 1 A^{(l+1)}=S^{(l)^{T}} A^{(l)} S^{(l)} \in \mathbb{R}^{n_{l+1} \times n_{l+1}} A(l+1)=S(l)TA(l)S(l)∈Rnl+1?×nl+1? A i j ( l + 1 ) A_{ij}^{(l+1)} Aij(l+1)?表示第 l + 1 l+1 l+1層cluster i和cluster j之間的連接強(qiáng)度 (2)分配矩陣的學(xué)習(xí)(Learning the assignment matrix) 下面介紹DIFFPOOL如何用公式上述兩個(gè)公式生成assignment矩陣 S ( l ) S^{(l)} S(l)和embedding矩陣 Z ( l ) Z^{(l)} Z(l): Z ( l ) = G N N l , ?embed? ( A ( l ) , X ( l ) ) (5) \tag{5} Z^{(l)}=\mathrm{GNN}_{l, \text { embed }}\left(A^{(l)}, X^{(l)}\right) Z(l)=GNNl,?embed??(A(l),X(l))(5) S ( l ) = softmax ? ( GNN ? l , pool ? ( A ( l ) , X ( l ) ) ) (6) \tag{6} S^{(l)}=\operatorname{softmax}\left(\operatorname{GNN}_{l, \operatorname{pool}}\left(A^{(l)}, X^{(l)}\right)\right) S(l)=softmax(GNNl,pool?(A(l),X(l)))(6) 其中: GNN ? l , pool ? \operatorname{GNN}_{l, \operatorname{pool}} GNNl,pool?表示第 l l l層的pooling GNN GNN ? l , pool ? \operatorname{GNN}_{l, \operatorname{pool}} GNNl,pool?的輸出維數(shù)對(duì)應(yīng)于第 l 層預(yù)定義的最大cluster數(shù),是模型的超參數(shù)使用cluster的鄰接矩陣 A ( l ) A^{(l)} A(l)和特征矩陣 X ( l ) X^{(l)} X(l)生成一個(gè)assignment矩陣這兩個(gè)GNN使用相同的輸入數(shù)據(jù),但具有不同的參數(shù),并扮演不同的角色:embedding GNN為這一層的輸入節(jié)點(diǎn)生成新的embedding,而pooling GNN生成從輸入節(jié)點(diǎn)到 n l + 1 n_{l+1} nl+1?個(gè)cluster的概率。 在倒數(shù)第二層,即L-1層時(shí)令assignment矩陣是一個(gè)全為1的向量,也就是說(shuō)所有在最后的L層的節(jié)點(diǎn)都會(huì)被分到一個(gè)cluster,生成對(duì)應(yīng)于整圖的一個(gè)embedding向量。這個(gè)embedding向量可以作為可微分類器(如softmax層)的特征輸入,整個(gè)系統(tǒng)可以使用隨機(jī)梯度下降進(jìn)行端到端的訓(xùn)練。 總結(jié)一下DiffPool的優(yōu)點(diǎn): (1)可以學(xué)習(xí)層次化的pooling策略; (2)可以學(xué)習(xí)到圖的層次化表示; (3)可以以端到端的方式被各種圖神經(jīng)網(wǎng)絡(luò)整合。 DiffPool也有其局限性,分配矩陣需要很大的空間去存儲(chǔ),空間復(fù)雜度為 O ( k V 2 ) O(kV^2) O(kV2), k k k為池化層的層數(shù),所以無(wú)法處理很大的圖。 5. 實(shí)現(xiàn)圖神經(jīng)網(wǎng)絡(luò)的步驟GNN 用起來(lái)相當(dāng)簡(jiǎn)單。事實(shí)上,實(shí)現(xiàn)它們涉及到以下四個(gè)步驟: 給定一個(gè)圖,首先將節(jié)點(diǎn)轉(zhuǎn)換為循環(huán)單元,將邊轉(zhuǎn)換為前饋神經(jīng)網(wǎng)絡(luò);接著為所有節(jié)點(diǎn)執(zhí)行 n 次近鄰聚合(也就是消息傳遞);然后再在所有節(jié)點(diǎn)的嵌入向量上求和以得到圖表征 H;最后可以完全跳過 H 直接向更高層級(jí)進(jìn)發(fā)或者也可使用 H 來(lái)表征該圖的獨(dú)有性質(zhì)。 6. 推薦書籍《Graphs, Networks and Algorithms》 第四版:在過去的幾十年里,組合優(yōu)化和圖論——作為組合學(xué)的整個(gè)領(lǐng)域——經(jīng)歷了特別快速的發(fā)展。這一事實(shí)有多種原因;一個(gè)是,例如,應(yīng)用組合論證已經(jīng)變得越來(lái)越普遍。然而,數(shù)學(xué)之外的兩個(gè)發(fā)展可能更為重要:首先,組合優(yōu)化的許多問題直接產(chǎn)生于工程和管理的日常實(shí)踐;確定交通或通信網(wǎng)絡(luò)中最短或最可靠的路徑,最大或相容的流量,或最短的線路;規(guī)劃交通網(wǎng)絡(luò)的連接;協(xié)調(diào)項(xiàng)目;解決供需問題。第二,隨著越來(lái)越高效的計(jì)算機(jī)系統(tǒng)的發(fā)展,那些屬于運(yùn)籌學(xué)的任務(wù)的實(shí)際實(shí)例已經(jīng)可以得到。此外,組合優(yōu)化問題對(duì)復(fù)雜性理論也很重要,復(fù)雜性理論是數(shù)學(xué)和理論計(jì)算機(jī)科學(xué)的交叉領(lǐng)域,涉及算法分析。組合優(yōu)化是數(shù)學(xué)中令人著迷的一部分,它的魅力——至少對(duì)我來(lái)說(shuō)——很大程度上來(lái)自于它的跨學(xué)科性和實(shí)用性。本書主要介紹了可以用圖論方法表述和處理的組合優(yōu)化部分;既不考慮線性規(guī)劃理論,也不考慮多面體組合理論。 https://www.springer.com/gp/book/9783642322778 |
【本文地址】
| 今日新聞 |
| 推薦新聞 |
| 專題文章 |
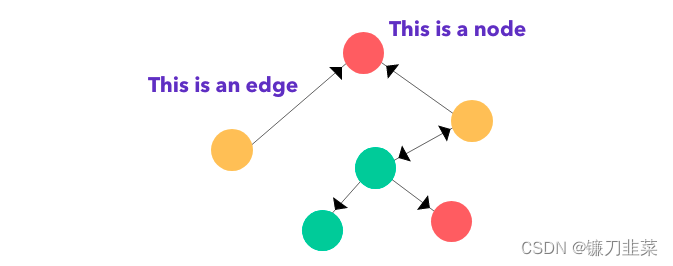 邊上面的黑色尖頭表示節(jié)點(diǎn)之間的關(guān)系類型,其可表明一個(gè)關(guān)系是雙向的還是單向的。圖有兩種主要類型:有向圖和無(wú)向圖。在有向圖中,節(jié)點(diǎn)之間的連接存在方向;而無(wú)向圖的連接順序并不重要。有向圖既可以是單向的,也可以是雙向的。
邊上面的黑色尖頭表示節(jié)點(diǎn)之間的關(guān)系類型,其可表明一個(gè)關(guān)系是雙向的還是單向的。圖有兩種主要類型:有向圖和無(wú)向圖。在有向圖中,節(jié)點(diǎn)之間的連接存在方向;而無(wú)向圖的連接順序并不重要。有向圖既可以是單向的,也可以是雙向的。 節(jié)點(diǎn)表示用戶,邊則表示兩個(gè)實(shí)體之間的連接/關(guān)系。真實(shí)的社交網(wǎng)絡(luò)圖往往更加龐大和復(fù)雜!
節(jié)點(diǎn)表示用戶,邊則表示兩個(gè)實(shí)體之間的連接/關(guān)系。真實(shí)的社交網(wǎng)絡(luò)圖往往更加龐大和復(fù)雜! 為了簡(jiǎn)單起見,假設(shè)圖節(jié)點(diǎn)的特征向量是當(dāng)前節(jié)點(diǎn)的索引的one-hot編碼。類似地,其標(biāo)簽(或類別)可設(shè)為節(jié)點(diǎn)的顏色(綠、紅、黃)。那么這個(gè)圖看起來(lái)會(huì)是這樣:
為了簡(jiǎn)單起見,假設(shè)圖節(jié)點(diǎn)的特征向量是當(dāng)前節(jié)點(diǎn)的索引的one-hot編碼。類似地,其標(biāo)簽(或類別)可設(shè)為節(jié)點(diǎn)的顏色(綠、紅、黃)。那么這個(gè)圖看起來(lái)會(huì)是這樣:  節(jié)點(diǎn)的順序其實(shí)并不重要。
節(jié)點(diǎn)的順序其實(shí)并不重要。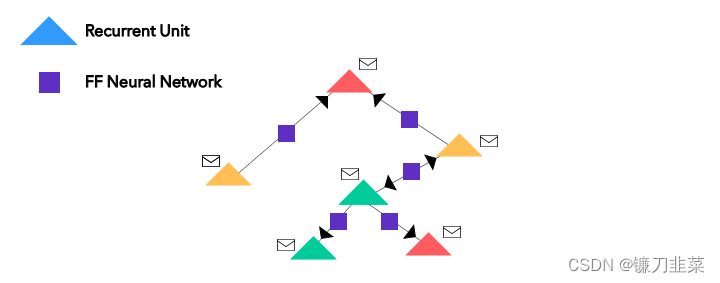 其中的信封符號(hào)只是每個(gè)節(jié)點(diǎn)的 one-hot 編碼的向量(嵌入)。
其中的信封符號(hào)只是每個(gè)節(jié)點(diǎn)的 one-hot 編碼的向量(嵌入)。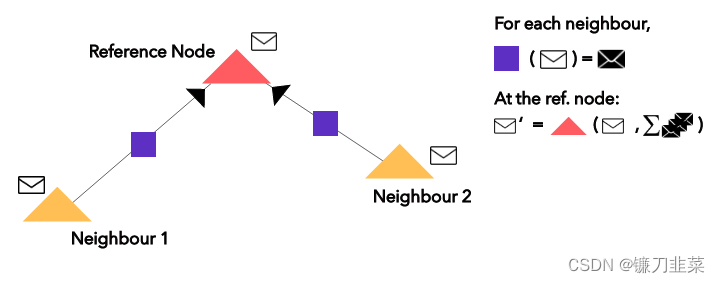 紫色方塊是一個(gè)應(yīng)用于來(lái)自近鄰節(jié)點(diǎn)的嵌入(白色信封)上的簡(jiǎn)單前饋神經(jīng)網(wǎng)絡(luò);紅色三角形是應(yīng)用于當(dāng)前嵌入(白色信封)和邊神經(jīng)網(wǎng)絡(luò)輸出(黑色信封)之和上的循環(huán)函數(shù),以得到新的嵌入(最上面的白色信封)。
紫色方塊是一個(gè)應(yīng)用于來(lái)自近鄰節(jié)點(diǎn)的嵌入(白色信封)上的簡(jiǎn)單前饋神經(jīng)網(wǎng)絡(luò);紅色三角形是應(yīng)用于當(dāng)前嵌入(白色信封)和邊神經(jīng)網(wǎng)絡(luò)輸出(黑色信封)之和上的循環(huán)函數(shù),以得到新的嵌入(最上面的白色信封)。 圖1 典型的圖神經(jīng)網(wǎng)絡(luò)
圖1 典型的圖神經(jīng)網(wǎng)絡(luò)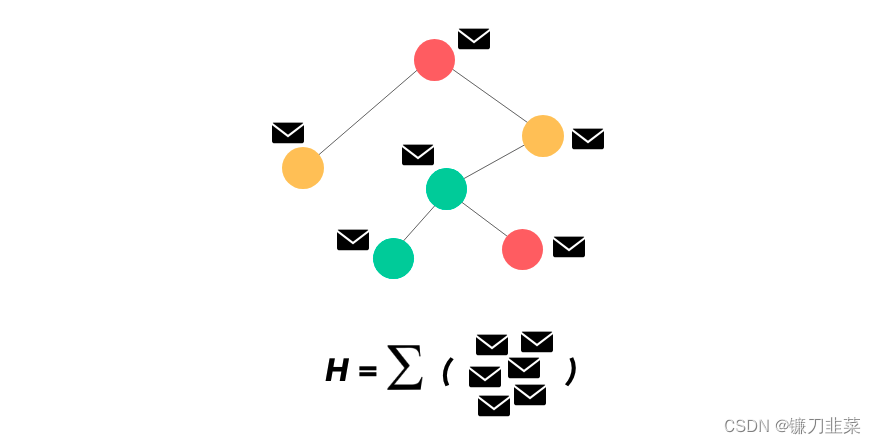 這是經(jīng)過 n 次重復(fù)消息傳遞之后帶有已完全更新的嵌入向量的最終圖。可以將所有節(jié)點(diǎn)的表征加到一起得到 H。
這是經(jīng)過 n 次重復(fù)消息傳遞之后帶有已完全更新的嵌入向量的最終圖。可以將所有節(jié)點(diǎn)的表征加到一起得到 H。 圖2 Thomas N. Kipf等人提出GCN
圖2 Thomas N. Kipf等人提出GCN 這種聚合方式實(shí)際上就是在對(duì)鄰接求和取平均。而
D
~
?
1
2
A
~
D
~
?
1
2
\tilde {D}^{-\frac{1}{2}}\tilde {A}\tilde {D}^{-\frac{1}{2}}
D~?21?A~D~?21?這種歸一化方式,將不再單單地對(duì)領(lǐng)域節(jié)特征點(diǎn)取平均,它不僅考慮了節(jié)點(diǎn)
i
i
i的度,也考慮了鄰接節(jié)點(diǎn)
j
j
j的度,當(dāng)鄰居節(jié)點(diǎn)
j
j
j 度數(shù)較大時(shí),它在聚合時(shí)貢獻(xiàn)地會(huì)更少。這也比較好理解,存在B->Ah′
1?,h′
2?,...,h′
N?},h′
i?∈RF′,其中,
F
′
F'
F′表示新的節(jié)點(diǎn)特征向量維度(可以不等于
F
F
F)。
這種聚合方式實(shí)際上就是在對(duì)鄰接求和取平均。而
D
~
?
1
2
A
~
D
~
?
1
2
\tilde {D}^{-\frac{1}{2}}\tilde {A}\tilde {D}^{-\frac{1}{2}}
D~?21?A~D~?21?這種歸一化方式,將不再單單地對(duì)領(lǐng)域節(jié)特征點(diǎn)取平均,它不僅考慮了節(jié)點(diǎn)
i
i
i的度,也考慮了鄰接節(jié)點(diǎn)
j
j
j的度,當(dāng)鄰居節(jié)點(diǎn)
j
j
j 度數(shù)較大時(shí),它在聚合時(shí)貢獻(xiàn)地會(huì)更少。這也比較好理解,存在B->Ah′
1?,h′
2?,...,h′
N?},h′
i?∈RF′,其中,
F
′
F'
F′表示新的節(jié)點(diǎn)特征向量維度(可以不等于
F
F
F)。 為了將輸入特征轉(zhuǎn)換為高維特征(增維)以獲得足夠的表達(dá)能力,每個(gè)節(jié)點(diǎn)將經(jīng)過一個(gè)共享的線性變換,該模塊的參數(shù)用權(quán)重矩陣
W
∈
R
F
′
×
F
W\in \mathbb{R}^{F'\times F}
W∈RF′×F來(lái)表示,對(duì)某個(gè)節(jié)點(diǎn)做線性變換可表示為
W
h
?
i
∈
R
F
′
W\vec{h}_i\in \mathbb{R}^{F'}
Wh
i?∈RF′。這是一種常見的特征增強(qiáng)(feature augment)方法。
為了將輸入特征轉(zhuǎn)換為高維特征(增維)以獲得足夠的表達(dá)能力,每個(gè)節(jié)點(diǎn)將經(jīng)過一個(gè)共享的線性變換,該模塊的參數(shù)用權(quán)重矩陣
W
∈
R
F
′
×
F
W\in \mathbb{R}^{F'\times F}
W∈RF′×F來(lái)表示,對(duì)某個(gè)節(jié)點(diǎn)做線性變換可表示為
W
h
?
i
∈
R
F
′
W\vec{h}_i\in \mathbb{R}^{F'}
Wh
i?∈RF′。這是一種常見的特征增強(qiáng)(feature augment)方法。 為了使不同節(jié)點(diǎn)間的注意力系數(shù)易于比較,使用softmax函數(shù)對(duì)所有對(duì)于節(jié)點(diǎn)
i
i
i的注意力系數(shù)進(jìn)行歸一化。上述注意力機(jī)制,采用共享權(quán)重線性變換、Masked self attention 和 LeakyReLU非線性(negative input slope α = 0.2)歸一化后的計(jì)算公式如下,其中 T表示轉(zhuǎn)置,||表示拼接:
為了使不同節(jié)點(diǎn)間的注意力系數(shù)易于比較,使用softmax函數(shù)對(duì)所有對(duì)于節(jié)點(diǎn)
i
i
i的注意力系數(shù)進(jìn)行歸一化。上述注意力機(jī)制,采用共享權(quán)重線性變換、Masked self attention 和 LeakyReLU非線性(negative input slope α = 0.2)歸一化后的計(jì)算公式如下,其中 T表示轉(zhuǎn)置,||表示拼接: 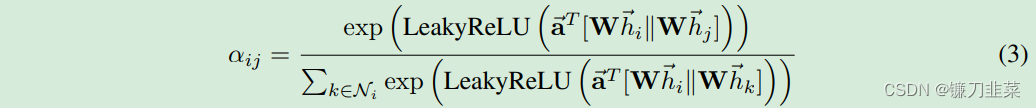 在得到歸一化的注意力系數(shù)之后,可以通過對(duì)鄰接節(jié)點(diǎn)特征的線性組合經(jīng)過一個(gè)非線性激活函數(shù)來(lái)更新節(jié)點(diǎn)自身的特征作為輸出:
h
′
?
i
=
σ
(
∑
j
∈
N
i
α
i
j
W
h
?
j
)
\vec{h'}_i=\sigma (\sum_{j\in\mathcal{N}_i}\alpha _{ij}W\vec{h}_j)
h′
i?=σ(j∈Ni?∑?αij?Wh
j?)
在得到歸一化的注意力系數(shù)之后,可以通過對(duì)鄰接節(jié)點(diǎn)特征的線性組合經(jīng)過一個(gè)非線性激活函數(shù)來(lái)更新節(jié)點(diǎn)自身的特征作為輸出:
h
′
?
i
=
σ
(
∑
j
∈
N
i
α
i
j
W
h
?
j
)
\vec{h'}_i=\sigma (\sum_{j\in\mathcal{N}_i}\alpha _{ij}W\vec{h}_j)
h′
i?=σ(j∈Ni?∑?αij?Wh
j?) 如果我們?cè)谧詈笠粚樱A(yù)測(cè)層)使用Multi-head attention mechanism,需要把輸出進(jìn)行平均化,再使用非線性函數(shù)(softmax或logistic sigmoid),公式如下:
如果我們?cè)谧詈笠粚樱A(yù)測(cè)層)使用Multi-head attention mechanism,需要把輸出進(jìn)行平均化,再使用非線性函數(shù)(softmax或logistic sigmoid),公式如下:  多頭注意力本質(zhì)是引入并行的幾個(gè)獨(dú)立的注意力機(jī)制,可以提取信息中的多重含義,防止過擬合。
多頭注意力本質(zhì)是引入并行的幾個(gè)獨(dú)立的注意力機(jī)制,可以提取信息中的多重含義,防止過擬合。 這其中比較經(jīng)典的模型有GraphSAGE、Graph Auto-Encoder(GAE)等,GraphSAGE就是一種很好的無(wú)監(jiān)督表示學(xué)習(xí)的方法,前面已經(jīng)介紹了,這里就不贅述。
這其中比較經(jīng)典的模型有GraphSAGE、Graph Auto-Encoder(GAE)等,GraphSAGE就是一種很好的無(wú)監(jiān)督表示學(xué)習(xí)的方法,前面已經(jīng)介紹了,這里就不贅述。 編碼器(Encoder)采用簡(jiǎn)單的三層GCN網(wǎng)絡(luò),解碼器(Encoder)計(jì)算兩點(diǎn)之間存在邊的概率來(lái)重構(gòu)圖,損失函數(shù)包括生成圖和原始圖之間的距離度量,以及節(jié)點(diǎn)表示向量分布和正態(tài)分布的KL-散度兩部分。具體公式如圖12所示:
編碼器(Encoder)采用簡(jiǎn)單的三層GCN網(wǎng)絡(luò),解碼器(Encoder)計(jì)算兩點(diǎn)之間存在邊的概率來(lái)重構(gòu)圖,損失函數(shù)包括生成圖和原始圖之間的距離度量,以及節(jié)點(diǎn)表示向量分布和正態(tài)分布的KL-散度兩部分。具體公式如圖12所示:  另外為了做比較,論文作者還提出了圖自編碼器(Graph Auto-Encoder),相比于變分圖的自編碼器,圖自編碼器就簡(jiǎn)單多了,Encoder是兩層GCN,Loss只包含Reconstruction Loss。
另外為了做比較,論文作者還提出了圖自編碼器(Graph Auto-Encoder),相比于變分圖的自編碼器,圖自編碼器就簡(jiǎn)單多了,Encoder是兩層GCN,Loss只包含Reconstruction Loss。 Graph pooling的方法有很多,如簡(jiǎn)單的max pooling和mean pooling,然而這兩種pooling不高效而且忽視了節(jié)點(diǎn)的順序信息;這里介紹一種方法:Differentiable Pooling (DiffPool)。
Graph pooling的方法有很多,如簡(jiǎn)單的max pooling和mean pooling,然而這兩種pooling不高效而且忽視了節(jié)點(diǎn)的順序信息;這里介紹一種方法:Differentiable Pooling (DiffPool)。