| 一文帶你搞懂匈牙利算法 | 您所在的位置:網(wǎng)站首頁 › 屬羊今天錢財(cái) › 一文帶你搞懂匈牙利算法 |
一文帶你搞懂匈牙利算法
|
一文帶你搞懂匈牙利算法
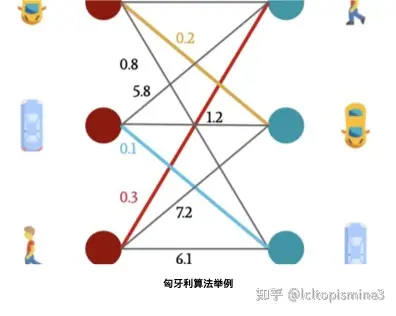
最近在研究一個比較有意思的應(yīng)用—車輛追蹤算法。傳統(tǒng)的車輛追蹤算法是基于檢測器檢出車輛,之后使用卡爾曼濾波和匈牙利算法來進(jìn)行位置預(yù)測與數(shù)據(jù)級聯(lián)的。關(guān)于卡爾曼濾波,我之前已經(jīng)寫過一篇文章進(jìn)行了詳細(xì)的介紹;最近則是在研究匈牙利算法是如何工作的。這里簡單的記錄一下相關(guān)原理。 匈牙利算法是一種在多項(xiàng)式時間內(nèi)求解任務(wù)分配問題的組合優(yōu)化算法,廣泛應(yīng)用在運(yùn)籌學(xué)領(lǐng)域。 美國數(shù)學(xué)家哈羅德·庫恩于1955年提出該算法。之所以被稱作匈牙利算法,是因?yàn)樗惴ê艽笠徊糠质腔谝郧靶傺览麛?shù)學(xué)家Dénes K?nig(1884-1944)和Jen? Egerváry(1891-1958)的工作上創(chuàng)建起來的。 在車輛追蹤中,匈牙利算法(Hungarian Algorithm)與KM算法(Kuhn-Munkres Algorithm)都是用來解決多目標(biāo)跟蹤中的數(shù)據(jù)關(guān)聯(lián)問題,而數(shù)據(jù)關(guān)聯(lián)問題,亦可轉(zhuǎn)化為求解二分圖的最大匹配問題。二分圖的最大匹配問題聽起來很繞口,這里如何理解呢?換句話說,就是求解任務(wù)分配問題,也叫指派問題,即n項(xiàng)任務(wù),對應(yīng)分配給n個人去做,應(yīng)該由哪個人來完成哪項(xiàng)任務(wù),能夠使完成效率最高。 這里舉一個例子
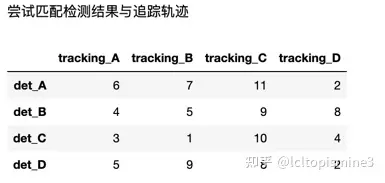
從圖上可以看到,不同的車和人,之間的距離是不一樣的。那么如果正確的把對應(yīng)的車和對應(yīng)的人匹配起來呢?這時候就需要用到匈牙利算法。 一個關(guān)于匈牙利算法的例子這里我們使用一個例子來說明如何使用匈牙利算法 假設(shè)你有4個檢測框(簡寫為det),對應(yīng)于四個相應(yīng)的追蹤軌跡(簡寫為tracking), 給定相應(yīng)之間的距離(稍后會講到怎么算這個距離),那么如何匹配檢測框與對應(yīng)的追蹤軌跡呢?
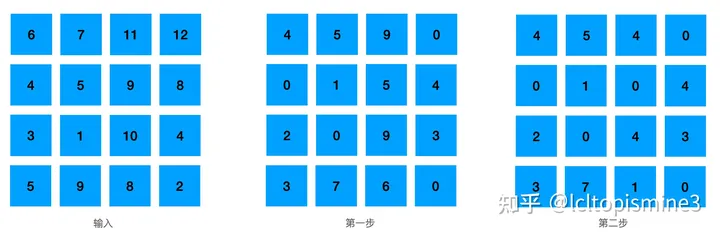
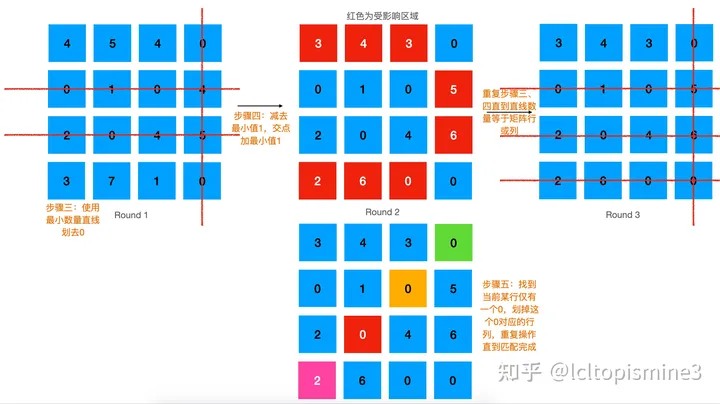
我們可以采用這樣幾個步驟來進(jìn)行匹配 按照行,減去本行最小值 按照列,減去本列最小值 嘗試以最少數(shù)量的線條劃掉所有零;如果這個數(shù)量大于等于矩陣的行列數(shù),那么跳到第五步 在剩下的矩陣中,減去最小值;如果有零被交叉,那么把這個最小值加上去,然后重復(fù)第三步 從只有一個零的行開始一一對應(yīng),對應(yīng)完則整個行列刪除
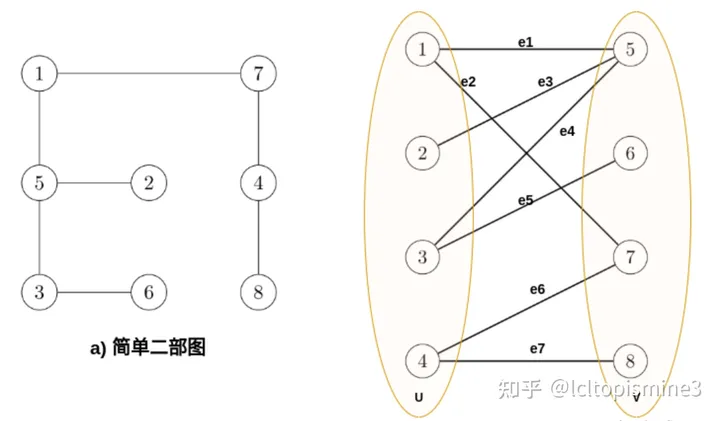
詳細(xì)的執(zhí)行步驟可以看一下這里的兩張圖,有比較清晰的描述。 最終結(jié)果: det_A->D det_B->A det_C->B det_D->C, 這里 -> 代表 “匹配”的意思。 額外要注意的是,這里我們求解的矩陣是N * N的,如果對應(yīng)矩陣是 M * N的話,需要給少的維度補(bǔ)齊,補(bǔ)的值是當(dāng)前矩陣中的最大值即可。 匈牙利算法原理與實(shí)現(xiàn)接下來,我們簡單聊一下匈牙利算法的原理和實(shí)現(xiàn)。 匈牙利算法一般是在二分圖(Bipartite graph)這樣的數(shù)據(jù)結(jié)構(gòu)上實(shí)現(xiàn)的。這種圖的名字可以看到,會把圖中元素一分為二,其中頂點(diǎn)分為兩兩不相交的集合,并且同屬于一個集合內(nèi)的點(diǎn)兩兩不相連。
那么如何基于二分圖(也叫二部圖)判斷匹配呢?這里我們說兩條邊匹配,即為存在兩條邊e1,e2,有e1,e2的頂點(diǎn)不相交,即為成功匹配。反之,如果相交了,代表的情況就是同一個人完成兩個任務(wù),這不符合匹配的要求,具體例子可以看下圖。
這里,我們有邊 e1 連接 點(diǎn)1和點(diǎn)5, e6連接 點(diǎn)4和點(diǎn)7,且各點(diǎn)之間不相交;紅色邊表示成功的匹配,被稱為匹配邊,匹配邊所連接的點(diǎn)被稱為匹配點(diǎn)。同樣可以定義非匹配邊和非匹配點(diǎn)(也就是頂點(diǎn)相交) 接下來,我們再給出最大匹配的定義:如果給定的二分圖里面,有若干邊不相交(形成若干匹配),且匹配數(shù)量達(dá)到這個二分圖里所有可能匹配的最大值,那么我們認(rèn)為這個二分圖對應(yīng)的匹配達(dá)到最大匹配(Maximum Matching)。圖中 {e2,e3,e5,e7} 即為其中一組最大匹配。
此外有關(guān)于二分圖(也屬于圖的定義),還有兩個常常提到的定義,這里簡單做一下介紹。 交錯路徑:圖匹配結(jié)果中,如果相鄰兩條邊性質(zhì)不同,也就是出現(xiàn)匹配邊->非匹配邊->匹配邊 相互交錯的情況,那么我們說存在交錯路徑。假設(shè) {e2, e7}相互匹配,我們有 {e1,e2,e6,e7}為交錯路徑。 增廣路徑:如果一條路徑的首尾是非匹配點(diǎn),路徑中除此之外(如果有)其他的點(diǎn)均是匹配點(diǎn),那么這條路徑就是一條增廣路徑(Agumenting path)。也就是說,從一個非匹配點(diǎn)出發(fā),走交錯路徑到另一個非匹配點(diǎn)(保證了兩邊的邊為非匹配邊)。這里假設(shè){e1, e6}相互匹配,我們有 {e7,e6,e2,e1,e3}為增廣路徑。 從增廣路徑的定義可以看到,增廣路徑的首尾是非匹配點(diǎn)。因此,增廣路徑的第一條和最后一條邊,必然是非匹配邊;由交錯路徑的定義可知,增廣路徑從非匹配邊開始,匹配邊和非匹配邊依次交替,最后由非匹配邊結(jié)束。這樣一來,增廣路徑中非匹配邊的數(shù)目總比匹配邊大 1。考慮置換增廣路徑中的匹配邊和非匹配邊,由于增廣路徑的首尾是非匹配點(diǎn),其余則是匹配點(diǎn),這樣的置換不會影響原匹配中其他的匹配邊和匹配點(diǎn),因而不會破壞匹配;而增廣路徑的置換,可使匹配的邊數(shù)加1,得到比原有匹配更大的匹配。 由于二分圖的最大匹配必然存在(比如,上限是包含所有頂點(diǎn)的完全匹配),所以,在任意匹配的基礎(chǔ)上,如果有辦法不斷地搜尋出增廣路徑,直到最終我們找不到新的增廣路徑為止。具體來說,每次找到增廣路徑,就嘗試進(jìn)行替換,使得匹配邊數(shù)+1。最后就有可能得到二分圖的一個最大匹配。這也是匈牙利算法的設(shè)計(jì)思路。 這里我們再舉一個例子來進(jìn)一步理解這個問題。
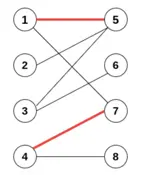
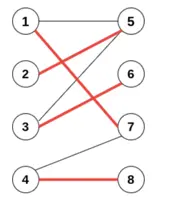
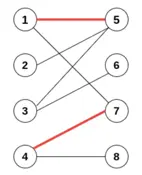
這里假設(shè)1-4是任務(wù), 5-8是對應(yīng)要干活的人,我們對應(yīng)的可以這么分配任務(wù):5->2, 6->3, 7->4 這樣子做之后,只有8無法分到任務(wù),這個時候并沒有實(shí)現(xiàn)最佳匹配。因此,我們進(jìn)一步的考慮交錯路徑 1->7; 7->4; 4->8中間是匹配邊,其余是非匹配邊,而且非匹配=匹配邊+1。這時我們嘗試交換匹配邊與非匹配邊,則有1->7, 4->8匹配, 這就找到了最大匹配。 匈牙利算法代碼示例這里提供一個使用python已有庫計(jì)算匈牙利算法的代碼片段,輸入數(shù)據(jù)和“一個關(guān)于匈牙利算法的例子”一節(jié)中的輸入數(shù)據(jù)一樣,我們把這個輸入數(shù)據(jù)叫做 cost_matrix。 import numpy as np from scipy.optimize import linear_sum_assignment cost_matrix = assignment.values.copy() print("cost matrix is: ") print(cost_matrix) matches = linear_sum_assignment(cost_matrix) print("find available matches: {}”.format(matches)) 匈牙利算法中如何計(jì)算權(quán)重(距離)現(xiàn)在我們嘗試把匈牙利算法應(yīng)用的車輛追蹤任務(wù)上,這里主要介紹數(shù)據(jù)關(guān)聯(lián)相關(guān)的內(nèi)容。 使用匈牙利算法,最為重要的是去了解當(dāng)前追蹤問題對應(yīng)的cost matrix,也就是損失矩陣。那么如果對損失矩陣進(jìn)行計(jì)算呢?這里我們介紹三種常見的方法: * 基于歐氏距離進(jìn)行匹配;給定兩幀中目標(biāo)框的中心點(diǎn),直接計(jì)算其中心點(diǎn)的歐式距離,需要迭代MXN次。如果目標(biāo)形態(tài)發(fā)生變化,或目標(biāo)間有重疊,那么效果相應(yīng)的會受很大影響。 * 計(jì)算車輛之間的IOU值并進(jìn)行計(jì)算,取最大值為合理匹配。然而匈牙利算法的目標(biāo)是最小化損失,而IOU是越大越好,所以兩者不相符合。解決方法是,找到待求解矩陣中的最大值,依次減去全部元素,然后繼續(xù)求解即可 * 使用外觀相似度進(jìn)行判斷。可以加入了外觀信息,借用了ReID領(lǐng)域模型來提取特征,使用生成的特征來判斷相似度。這樣子的做法減少了ID switch。 實(shí)際進(jìn)行損失計(jì)算,會同時考慮2和3,加權(quán)進(jìn)行計(jì)算以獲取最終匹配結(jié)果。 小結(jié)匈牙利算法是一種二分圖匹配算法,常用于二分圖的最大匹配。數(shù)據(jù)追蹤任務(wù)中,可以使用匈牙利算法進(jìn)行數(shù)據(jù)關(guān)聯(lián),在物體勻速場景下配合卡爾曼濾波,會起到很好的作用。限于匈牙利算法本身是求二分圖下最大結(jié)果,與數(shù)據(jù)級聯(lián)要求的最小損失有沖突,實(shí)際使用是會額外追加限制或進(jìn)行條件轉(zhuǎn)化,使得匈牙利算法可以用于車輛追蹤場景下的最優(yōu)結(jié)果匹配。 匈牙利算法并不需要我們手寫代碼。在了解如何計(jì)算損失并可以生成損失矩陣的情況下,可以套用scipy或scikit-learn已有庫來直接求解,相對來說還是比較方便的。 |
【本文地址】
| 今日新聞 |
| 推薦新聞 |
| 專題文章 |