復(fù)指數(shù)信號(hào)e^jwt的圖像及性質(zhì)

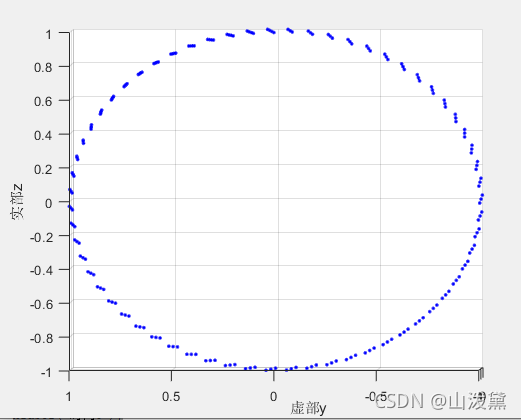
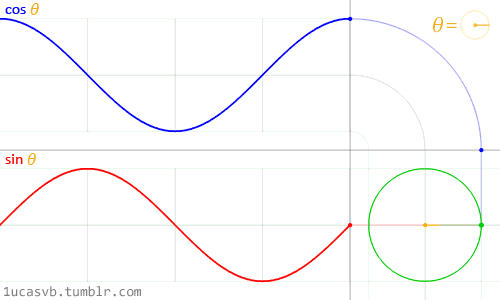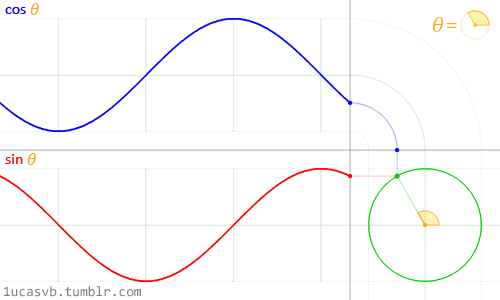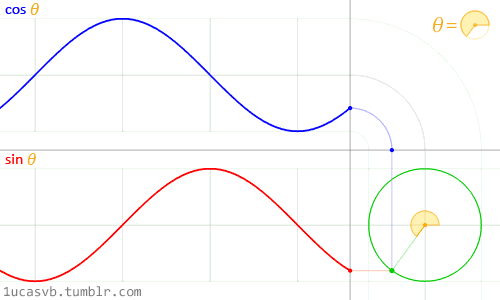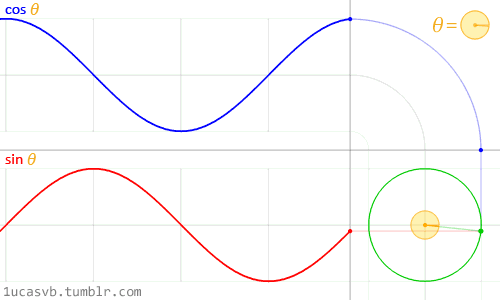
信號(hào)與系統(tǒng)、數(shù)字信號(hào)處理、信號(hào)分析，都離不開(kāi)傅里葉變換，而傅里葉變換又離不開(kāi) e j w t e^{jwt} ejwt。 關(guān)于 e j w t e^{jwt} ejwt，好像很熟悉，很了解，但問(wèn)你它是什么一個(gè)東西、有什么特點(diǎn)、相關(guān)的性質(zhì)屬性，你能馬上說(shuō)出來(lái)嗎？

首先， e j w t e^{jwt} ejwt中j是虛數(shù)單位，w一般當(dāng)做常量，t為變量。 關(guān)于虛數(shù)單位，應(yīng)當(dāng)回想起復(fù)數(shù)有關(guān)的知識(shí)，復(fù)數(shù)一般形如a+bj，可以在復(fù)平面用一根線表示，線的長(zhǎng)度表示復(fù)數(shù)的模，與實(shí)軸（橫軸）的夾角表示復(fù)數(shù)的相位。 既然 e j w t e^{jwt} ejwt有自變量t（正是因?yàn)橛辛藭r(shí)間變量， e j w t e^{jwt} ejwt也叫復(fù)指數(shù)信號(hào)），那應(yīng)當(dāng)可以畫(huà)出它的圖像。 談到 e j w t e^{jwt} ejwt的圖像，你腦海里浮現(xiàn)出什么？ 我腦海里竟想不出它的樣子。 anyway，而今邁步從頭越。

于是得到了 e j w t e^{jwt} ejwt的圖像

（注意上圖中的x坐標(biāo)的方向，與一般我們稿紙畫(huà)圖的方向不同，看大家的圖都不注明自變量的軸是哪個(gè)，難怪看暈了）

可以這樣理解，畫(huà)圖本來(lái)就是先讓自變量取一些值，然后在坐標(biāo)系中描點(diǎn)，最后連線。 上圖中的每一個(gè)點(diǎn)就是t取t0時(shí)， e j w t 0 e^{jwt0} ejwt0對(duì)應(yīng)的值，由歐拉公式可知 e j w t 0 e^{jwt0} ejwt0=cos(wt0)+jsin(wt0),得到的函數(shù)值是復(fù)數(shù)，復(fù)數(shù)要表示出來(lái)得需要兩個(gè)坐標(biāo)軸，這也是為什么畫(huà)出來(lái)是三維的。

然后對(duì)這幅圖進(jìn)行解析，也就是探究它的性質(zhì)。 首先，將所有的點(diǎn)在yoz平面上投影，得到的會(huì)是一個(gè)圓形。這是因?yàn)? e j w t e^{jwt} ejwt=cos(wt)+jsin(wt)，實(shí)部和虛部的平方和為1，所以 e j w t e^{jwt} ejwt在復(fù)平面上表示就是一個(gè)單位圓。

（matlab畫(huà)出來(lái)的三維圖是可以拖曳從不同角度觀察的，這是我拖到一個(gè)從x軸看過(guò)去的角度）

其次，關(guān)于w的物理意義和性質(zhì)，上面那副圖可以看著一個(gè)不斷螺旋前進(jìn)的軌跡圖，w即反應(yīng)了旋轉(zhuǎn)的快慢。

最后，關(guān)于 e j w t e^{jwt} ejwt。還可以看做一個(gè)單位長(zhǎng)度，逆時(shí)針旋轉(zhuǎn)的復(fù)平面旋轉(zhuǎn)向量。