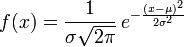高斯分布概率密度函數(shù)（PDF）和累積分布函數(shù)(CDF)

#高斯分布概率密度函數(shù)（PDF）和累積分布函數(shù)(CDF)| 來源: 網(wǎng)絡(luò)整理| 查看: 265

$f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{- {?{(x-\mu )^2 \over 2\sigma^2}}}$

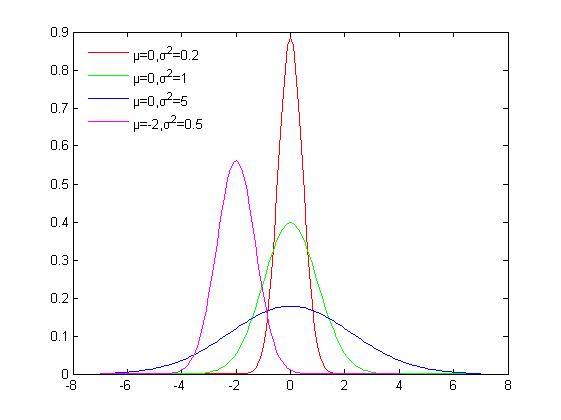
正態(tài)分布的期望值μ決定了其位置，其標(biāo)準(zhǔn)差σ決定了分布的幅度。因其曲線呈鐘形，因此人們又經(jīng)常稱之為鐘形曲線。我們通常所說的標(biāo)準(zhǔn)正態(tài)分布是μ = 0,σ = 1的正態(tài)分布（見右圖中綠色曲線）。

正態(tài)分布的概率密度函數(shù)均值為μ?方差為σ2?(或標(biāo)準(zhǔn)差σ)是高斯函數(shù)的一個(gè)實(shí)例：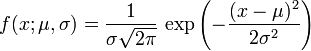

$f(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right)$ 累積分布函數(shù)

累積分布函數(shù)是指隨機(jī)變量X小于或等于x的概率，用密度函數(shù)表示為 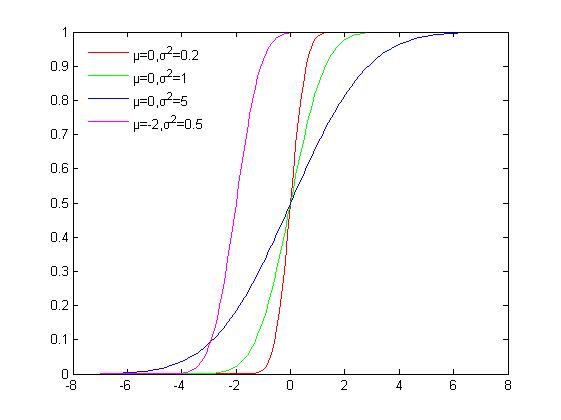$F(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x \exp \left( -\frac{(x - \mu)^2}{2\sigma^2}\ \right)\, dx.$

matlab實(shí)現(xiàn)代碼 function [ output_args ] = Normpropogation( input_args ) %NORM PROPOGATION Summary of this function goes here % Detailed explanation goes here x=-7:0.1:7; y1=normpdf(x,0,1); y2=normpdf(x,0,0.45); y3=normpdf(x,0,2.23); y4=normpdf(x,-2,0.71); %線型，顏色，點(diǎn)型，線寬 figure; plot(x,y2,'-r','LineWidth',1); hold on; plot(x,y1,'-g','LineWidth',1); hold on; plot(x,y3,'-b','LineWidth',1); hold on; plot(x,y4,'-m','LineWidth',1); hold on; % legend('','','','',1); legend('μ=0,σ^2=0.2','μ=0,σ^2=1','μ=0,σ^2=5','μ=-2,σ^2=0.5',2); legend boxoff; figure; z1=normcdf(x,0,0.45); z2=normcdf(x,0,1); z3=normcdf(x,0,2.23); z4=normcdf(x,-2,0.71); plot(x,z1,'-r',x,z2,'-g',x,z3,'-b',x,z4,'-m'); h=legend('μ=0,σ^2=0.2','μ=0,σ^2=1','μ=0,σ^2=5','μ=-2,σ^2=0.5',2); legend boxoff; end

【本文地址】

公司簡(jiǎn)介

聯(lián)系我們

今日新聞

推薦新聞

專題文章