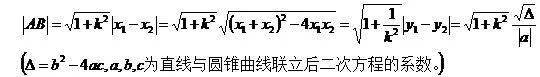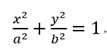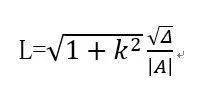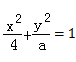| 全了!圓錐曲線解題技巧+7大題型匯總+常用公式推論! | 您所在的位置:網(wǎng)站首頁(yè) › 取名字大全免費(fèi)2021屬鼠的女孩子 › 全了!圓錐曲線解題技巧+7大題型匯總+常用公式推論! |
全了!圓錐曲線解題技巧+7大題型匯總+常用公式推論!
|
4、題型總結(jié) 圓錐曲線中常見題型總結(jié) 1、直線與圓錐曲線位置關(guān)系 這類問題主要采用分析判別式,有 △>0,直線與圓錐曲線相交; △=0,直線與圓錐曲線相切; △<0,直線與圓錐曲線相離. 若且a=0,b≠0,則直線與圓錐曲線相交,且有一個(gè)交點(diǎn). 注意:設(shè)直線方程時(shí)一定要考慮斜率不存在的情況,可單獨(dú)提前討論。 2、圓錐曲線與向量結(jié)合問題 這類問題主要利用向量的相等,平行,垂直去尋找坐標(biāo)間的數(shù)量關(guān)系,往往要和根與系數(shù)的關(guān)系結(jié)合應(yīng)用,體現(xiàn)數(shù)形結(jié)合的思想,達(dá)到簡(jiǎn)化計(jì)算的目的。 3、圓錐曲線弦長(zhǎng)問題 弦長(zhǎng)問題主要記住弦長(zhǎng)公式:設(shè)直線l與圓錐曲線C相交于A(x 1 ,y 1 ),B( x 2 ,y 2 )兩點(diǎn),則:
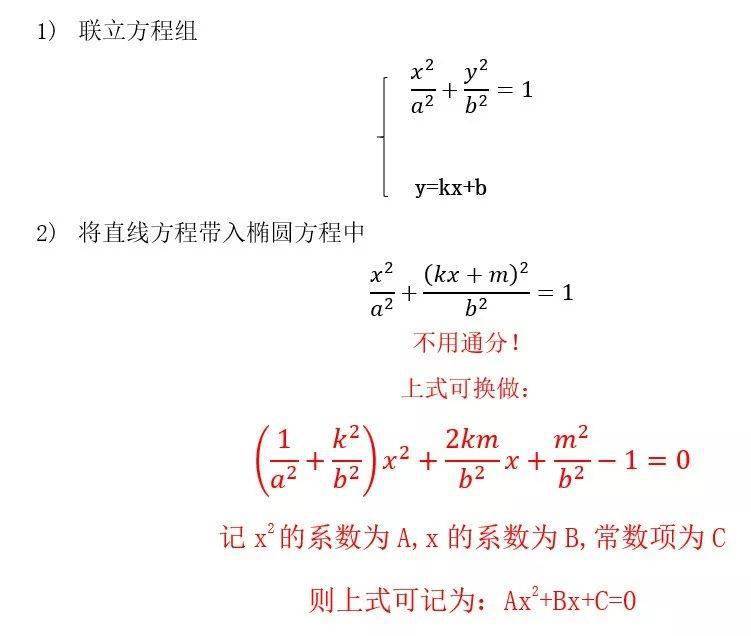
4、定點(diǎn)、定值問題 (1)定點(diǎn)問題可先運(yùn)用特殊值或者對(duì)稱探索出該定點(diǎn),再證明結(jié)論,即可簡(jiǎn)化運(yùn)算; (2)直接推理、計(jì)算,并在計(jì)算推理的過程中消去變量,從而得到定值. 5、最值、參數(shù)范圍問題 這類常見的解法有兩種:幾何法和代數(shù)法. (1)若題目的條件和結(jié)論能明顯體現(xiàn)幾何特征和意義,則考慮利用圖形性質(zhì)來解決,這就是幾何法; (2)若題目的條件和結(jié)論能體現(xiàn)一種明確的函數(shù)關(guān)系,則可首先建立起目標(biāo)函數(shù),再求這個(gè)函數(shù)的最值,這就是代數(shù)法. 在利用代數(shù)法解決最值與范圍問題時(shí)常從以下五個(gè)方面考慮: (1)利用判別式來構(gòu)造不等關(guān)系,從而確定參數(shù)的取值范圍; (2)利用已知參數(shù)的范圍,求新參數(shù)的范圍,解這類問題的核心是在兩個(gè)參數(shù)之間建立等量關(guān)系; (3)利用隱含或已知的不等關(guān)系建立不等式,從而求出參數(shù)的取值范圍; (4)利用基本不等式求出參數(shù)的取值范圍; (5)利用函數(shù)的值域的求法,確定參數(shù)的取值范圍. 6、軌跡問題 軌跡問題一般方法有三種:定義法,相關(guān)點(diǎn)法和參數(shù)法。 定義法: (1)判斷動(dòng)點(diǎn)的運(yùn)動(dòng)軌跡是否滿足某種曲線的定義; (2)設(shè)標(biāo)準(zhǔn)方程,求方程中的基本量 (3)求軌跡方程 相關(guān)點(diǎn)法: (1)分析題目:與動(dòng)點(diǎn)M(x,y)相關(guān)的點(diǎn)P(x 0 ,y 0 )在已知曲線上; (2)尋求關(guān)系式,x 0 =f(x,y),y 0 =g(x,y); (3)將x 0 ,y 0 代入已知曲線方程; (4)整理關(guān)于x,y的關(guān)系式得到M的軌跡方程。 參數(shù)法求軌跡的一般步驟: (1)選取參數(shù)k,用k表示動(dòng)點(diǎn)M的坐標(biāo); (2)得動(dòng)點(diǎn)M的軌跡的參數(shù)方程 (3)消去參數(shù)k得的M軌跡方程; (4)由k的范圍確定x,y的范圍,確保答案的準(zhǔn)確性和完備性。 7、探索型,存在性問題 這類問題通常先假設(shè)存在,然后進(jìn)行計(jì)算,最后再證明結(jié)果滿足條件得到結(jié)論。對(duì)于較難的題目,可從特殊情況入手,找到特殊點(diǎn)進(jìn)行分析驗(yàn)算,然后再得到一般性結(jié)論。 圓錐曲線簡(jiǎn)化技巧 1、給定一個(gè)橢圓和一條直線: 橢圓方程:
直線方程:y=kx+b
一般做法:
上面的運(yùn)算數(shù)不是有點(diǎn)復(fù)雜呢,那接著往下看看小數(shù)老師提供的計(jì)算技巧吧: 巧運(yùn)算:
2、此外,常用的兩個(gè)結(jié)論還有: 1、直線交橢圓的弦長(zhǎng):
(因?yàn)橹灰?lián)立了方程組,就一定要求判別式,將判別式代入這個(gè)式子求弦長(zhǎng)會(huì)比一般做法簡(jiǎn)單很多) 2、y 1 +y 2 =k(x 1 +x 2 )+2m y 1 y 2 =k 2 x 1 x 2 +km(x 1 +x 2 )+m 2 用此方法可大幅節(jié)省運(yùn)算時(shí)間,圓錐曲線是不是簡(jiǎn)單了不少呢? 例子 這里給出了兩道非常簡(jiǎn)單的例題,快用簡(jiǎn)潔的方法算一算吧。 1、若橢圓
與直線y=2x+5相切,求橢圓方程。 2、若直線y=kx+與橢圓交于不同的兩點(diǎn)A、B,O為坐標(biāo)原點(diǎn),且?>2,求k的取值范圍? 答案:1.a=9 2. 1/4 |
【本文地址】
| 今日新聞 |
| 推薦新聞 |
| 專題文章 |