| [無聊/科普向] 一篇關(guān)于《原神》抽卡概率/期望計(jì)算的正經(jīng)介紹 | 您所在的位置:網(wǎng)站首頁 › 原神 › [無聊/科普向] 一篇關(guān)于《原神》抽卡概率/期望計(jì)算的正經(jīng)介紹 |
[無聊/科普向] 一篇關(guān)于《原神》抽卡概率/期望計(jì)算的正經(jīng)介紹
|
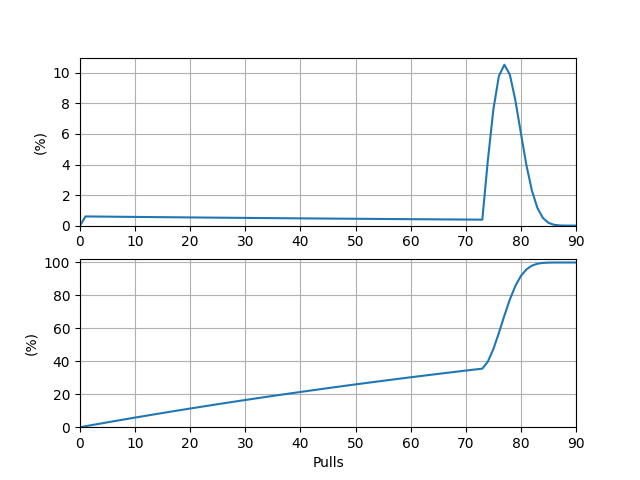
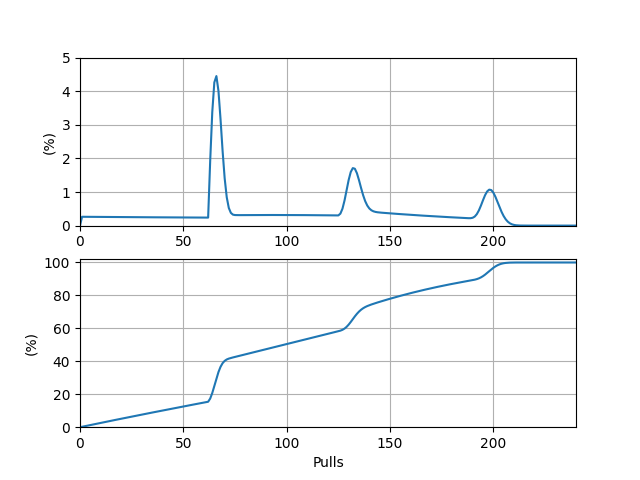
注:本文的正確性建立在目前廣為流傳的一份角色池與武器池單抽出貨概率數(shù)據(jù)之上,詳見文章 2.1 與 2.3 部分。 0 省流版角色池: 從零開始抽出一個(gè)五星角色期望抽數(shù):\(62.3\),中位抽數(shù):\(75\),最大概率抽數(shù):\(77\) 從零開始抽出一個(gè)目標(biāo) UP 五星角色期望抽數(shù):\(93.4\),中位抽數(shù):\(80\),最大概率抽數(shù):\(77\) 從零開始抽出滿命目標(biāo) UP 五星角色期望抽數(shù):\(654.1\),中位抽數(shù):\(653\),最大概率抽數(shù):\(644\)武器池: 從零開始抽出一把五星武器期望抽數(shù):\(53.3\),中位抽數(shù):\(64\),最大概率抽數(shù):\(66\) 從零開始抽出一把目標(biāo) UP 五星武器期望抽數(shù):\(105.7\),中位抽數(shù):\(98\),最大概率抽數(shù):\(66\) 從零開始抽出滿精目標(biāo) UP 五星武器期望抽數(shù):\(528.3\),中位抽數(shù):\(526\),最大概率抽數(shù):\(531\)能衡量“歐非”程度的最直接指標(biāo)是在前多少抽內(nèi)出貨的累計(jì)概率。上述六種情況的累積概率圖象見文章 2.2 與 2.3 對應(yīng)部分。 ? 1 文章介紹每一位熱衷于或受苦于在《原神》中抽卡的玩家都希望有一個(gè)直觀的指標(biāo)來幫助自己判斷自己的“歐非”程度。此時(shí),出貨關(guān)于抽數(shù)的概率分布以及出貨的期望次數(shù)成為了玩家們想要獲取到的信息。然而,大部分對概率與期望計(jì)算方法較為陌生的玩家面對游戲抽卡說明中的一堆數(shù)據(jù)表現(xiàn)得茫然。打開一些相關(guān)視頻的評論區(qū),你甚至能找到“抽卡保底數(shù)是 \(90\),所以期望出貨次數(shù)就是 \(90\)”這樣的評論。 本文的目的便是教會(huì)你正確計(jì)算出“省流版”部分中給出的所有數(shù)據(jù),并對《原神》抽卡模型的設(shè)計(jì)進(jìn)行一定的分析。 ? 2 主要流程 2.1 基礎(chǔ)數(shù)據(jù)獲取我們首先以角色 UP 池為例。 要想進(jìn)行具體的計(jì)算,我們首先需要獲取到單抽得到五星角色(即“出貨”)的概率。你可能會(huì)認(rèn)為,在祈愿說明中給出的“5 星角色祈愿的基礎(chǔ)概率為 \(0.600\%\)”正是我們所需要的數(shù)據(jù),實(shí)則不然。否則,如果每抽出貨的概率恒定,不會(huì)產(chǎn)生 \(90\) 抽保底的機(jī)制。 我們從一些地方可以獲取到這樣一個(gè)函數(shù):在累計(jì) \(i - 1\) 次抽卡未出貨后,第 \(i\) 次出貨的概率 \(p(i)\) 滿足 \[p(i) = \begin{cases}0.006, &i < 74,\\ \min\{1, p(i - 1) + 0.06\}, &i \geq 74.\end{cases} \]也即,前 \(73\) 次抽卡出貨的概率均為 \(0.6\%\),從第 \(74\) 抽開始,概率每抽增長 \(6\%\),直到 \(100\%\)。 這是目前網(wǎng)絡(luò)上流傳最廣泛的單抽概率數(shù)據(jù)。這一函數(shù)的深層來源我們不得而知,但它的確滿足這樣一些基本條件:以 \(0.6\%\) 作為基礎(chǔ)概率;保底為 \(90\) 抽;主觀上滿足抽卡的實(shí)際情形;表示形式較為簡單(這樣的概率的設(shè)計(jì)可能需要經(jīng)過較多推敲,但最終形式往往不會(huì)復(fù)雜)。我們姑且信之,并將其用于接下來的具體計(jì)算。 ? 2.2 具體計(jì)算 2.2.1 抽五星(忽略 UP 與否)角色我們首先計(jì)算從零開始抽卡出貨(僅考慮五星,忽略 UP 與否)關(guān)于抽數(shù)的概率分布。 設(shè) \(P(i)\) 表示從零開始恰好在第 \(i\) 抽出貨的概率。也許你可以輕易地寫出 \(P(i) = p(i) \cdot \prod\limits_{j = 1}^{i - 1}(1 - p(j))\),但在這里,我們用一個(gè)略顯復(fù)雜的方式表示它:再設(shè) \(f(i)\) 表示前 \(i\) 抽均沒有出貨的概率,從而列出方程組: \[\begin{cases}f(0) = 1, \\ f(i) = f(i - 1) \cdot (1 - p(i)), &i = 1, 2, \cdots, 90.\end{cases} \]并且有 \[P(i) = f(i - 1) \cdot p(i),~~~ i = 1, 2, \cdots, 90. \]這樣表示的好處我們很快就會(huì)看到。依據(jù)該方程組的形式,我們可以迭代地從 \(f(0)\) 開始依次計(jì)算 \(f(1), P(1), \cdots, f(90), P(90)\)。出貨的期望抽數(shù) \(E = \sum\limits_{i = 1}^{90}i \cdot P(i)\)。 我們簡單地寫一份 Python 代碼完成這一計(jì)算并輸出結(jié)果: import matplotlib.pyplot as plt import numpy as np PITY = 90 f = np.zeros(PITY) result = np.zeros(PITY + 1) single_rate = [0.006] * (PITY + 1) for i in range(74, 91): single_rate[i] = min((1.0, single_rate[i - 1] + 0.06)) ### Calculate f[0] = 1 for i in range(0, PITY): if i + 1 < PITY: f[i + 1] = f[i] * (1 - single_rate[i + 1]) result[i + 1] += f[i] * single_rate[i + 1] presum = np.zeros(PITY + 1) expect = 0 for i in range(1, PITY + 1): presum[i] = presum[i - 1] + result[i] expect += result[i] * i print("%i: %.10lf %.10lf" % (i, result[i], presum[i])) print("Expect: %.6lf" % (expect)) print("Debug: %.10lf" % (presum[PITY])) ### Draw function image fig, ax = plt.subplots(2, 1) ax[0].plot(np.arange(0, PITY + 1), result * 100) ax[1].plot(np.arange(0, PITY + 1), presum * 100) for i in range(0, 2): ax[i].grid(True) ax[i].set_ylabel('(%)') ax[i].set_xlim([0, PITY]) ax[0].set_ylim([0, 11]) ax[1].set_ylim([0, 102]) ax[1].set_xlabel('Pulls') plt.savefig('result') plt.show()輸出的期望抽數(shù) \(E_1 = 62.297332\)。\(P(i)\) 本身及其前綴和關(guān)于抽數(shù)的圖象如下(前綴和則表示在前 \(i\) 抽內(nèi)出貨的概率,這便是衡量“歐非”程度的最直接指標(biāo)):
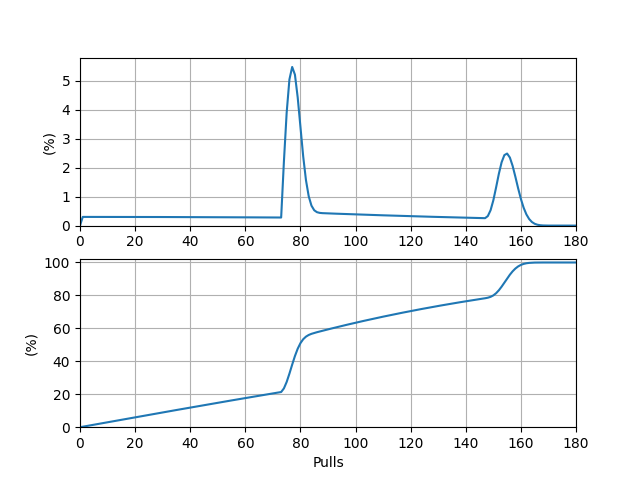
\(P(i)\) 圖象的峰值位于點(diǎn) \((77, 0.105)\) 處,這表明從零開始抽卡,最有可能在第 \(77\) 抽時(shí)出貨,概率約為 \(10.5\%\)。前綴和圖象的 \(50\%\) 對應(yīng)的抽數(shù)在 \(75\) 與 \(76\) 之間,距 \(75\) 更近,這表明中位抽數(shù)約為 \(75\)。至此,我們得到了“省流版”中的第一行數(shù)據(jù)。 ? 2.2.2 抽五星 UP 角色當(dāng)我們的目標(biāo)僅落在 UP 角色上時(shí),一些潛在的變量被引入了進(jìn)來:是否是大保底,以及若是大保底,又已經(jīng)累計(jì)了多少抽。在 2.2.1 部分中僅用一個(gè)變量 \(i\) 控制函數(shù) \(f\) 便不再可取。 仍設(shè) \(P(i)\) 表示從零開始恰好在第 \(i\) 抽出貨的概率。設(shè) \(f(i, j, x)(x \in \{0, 1\})\) 表示在前 \(i\) 抽沒有抽到目標(biāo) UP 角色,且保底情況為 \(x\)(\(0\) 為小保底,\(1\) 為大保底),保底累計(jì)抽數(shù)為 \(j\) 的概率。注意到當(dāng)處于小保底時(shí),有 \(0.5\) 的概率獲取到想要的 UP 角色,還有 \(0.5\) 的概率“歪”,因此可以列出方程組: \[\begin{cases} f(0, 0, 0) = 1, \\ f(i, j, x) = f(i - 1, j - 1, x) \cdot (1 - p(j)), &i = 1, \cdots, 180, ~ j = 1, \cdots, \min\{i, 90\}, ~ x = 0, 1, \\ f(i, 0, 1) = f(i - 1, i - 1, 0) \cdot p(i) \cdot 0.5, &i = 1, \cdots, 90. & & \end{cases}\]并且有 \[P(i) = \begin{cases} f(i - 1, i - 1, 0) \cdot p(i) \cdot 0.5 + \sum\limits_{j = 1}^{i}f(i - 1, j - 1, 1) \cdot p(i), & i \leq 90, \\ \sum\limits_{j = 1}^{90}f(i - 1, j - 1, 1) \cdot p(i), & i > 90. \end{cases}\]關(guān)于 \(f\) 的方程組中的第三個(gè)方程的含義為:如果在小保底階段抽中了五星角色,且為非 UP(概率為 \(0.5\)),則清空保底的累計(jì)抽數(shù),進(jìn)入大保底階段。 利用含參量 \(f\) 來計(jì)算 \(P\) 的好處此時(shí)便得以體現(xiàn)——當(dāng)需要考慮的情況變得復(fù)雜時(shí),我們可以通過增加參數(shù)變量來沿用之前的計(jì)算方法。\(f\) 仍然可以迭代計(jì)算,只需要分別從小到大枚舉 \(i, j\)。 沿用上面部分的代碼,做一些基礎(chǔ)修改后,核心計(jì)算部分如下: MAX_PULLS = 180 PITY = 90 f = np.zeros((MAX_PULLS, PITY, 2)) result = np.zeros(MAX_PULLS + 1) ### Calculate f[0][0][0] = 1 for i in range(0, MAX_PULLS): for j in range(0, min((i + 1, PITY))): if i + 1 < MAX_PULLS and j + 1 < PITY: for x in range(0, 2): f[i + 1][j + 1][x] += f[i][j][x] * (1 - single_rate[j + 1]) if i + 1 < MAX_PULLS: f[i + 1][0][1] += f[i][j][0] * single_rate[j + 1] * 0.5 result[i + 1] += f[i][j][0] * single_rate[j + 1] * 0.5 result[i + 1] += f[i][j][1] * single_rate[j + 1]輸出的期望抽數(shù) \(E_2 = 93.445998\)。事實(shí)上,它恰好為 \(E_1 = 62.297332\) 的 \(1.5\) 倍,這是因?yàn)槿粼谛”5纂A段就出 UP 角色,則期望抽數(shù)為 \(E_1\),而若在大保底階段才出 UP 角色,則期望抽數(shù)為 \(2E_1\),因此 \(E_2 = 0.5 \cdot E_1 + 0.5 \cdot 2E_1 = 1.5E_1\)。\(P(i)\) 本身及其前綴和關(guān)于抽數(shù)的圖象如下:
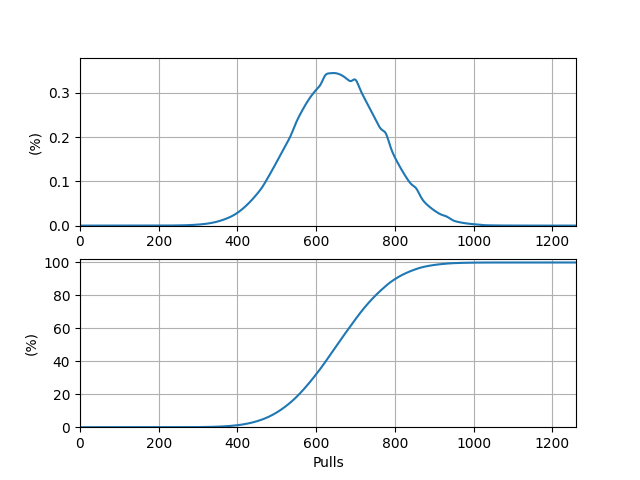
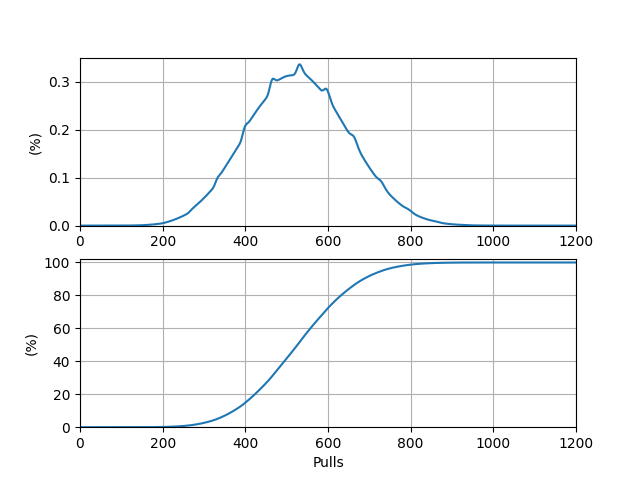
\(P(i)\) 圖象的峰值位于點(diǎn) \((77, 0.0548)\) 處,這表明從零開始抽卡,最有可能在第 \(77\) 抽時(shí)出目標(biāo) UP 角色,概率約為 \(5.48\%\)。前綴和圖象的 \(50\%\) 對應(yīng)的抽數(shù)在 \(79\) 與 \(80\) 之間,距 \(80\) 更近,這表明中位抽數(shù)約為 \(80\)。 ? 2.2.3 抽滿命五星 UP 角色對于 \(f\),在 2.2.2 部分的基礎(chǔ)上再引入一個(gè)參變量 \(k\) 表示已經(jīng)獲取的 UP 角色數(shù),即設(shè) \(f(i, j, k, x)(x \in \{0, 1\})\) 表示在前 \(i\) 抽沒有抽滿目標(biāo) UP 角色,保底情況為 \(x\)(\(0\) 為小保底,\(1\) 為大保底),保底累計(jì)抽數(shù)為 \(j\),且已經(jīng)獲得了 \(k\) 個(gè) UP 角色的概率。據(jù)此可以列出方程組(\(k = 0, 1, \cdots, 6\),其余變量范圍略): \[\begin{cases} f(0, 0, 0, 0) = 1, \\ f(i, j, k, x) = f(i - 1, j - 1, k, x) \cdot (1 - p(j)), \\ f(i, 0, k, 1) = \sum\limits_{j = 1}^{\min\{i, 90\}}f(i - 1, j - 1, k, 0) \cdot p(i) \cdot 0.5,\\ f(i, 0, k, 0) = \sum\limits_{j = 1}^{\min\{i, 90\}}f(i - 1, j - 1, k - 1, 0) \cdot p(i) \cdot 0.5 + f(i - 1, j - 1, k - 1, 1) \cdot p(i) \end{cases}\]并且有 \[P(i) = \sum_{j = 1}^{\min\{i, 90\}}f(i - 1, j - 1, 6, 0) \cdot p(i) \cdot 0.5 + f(i - 1, j - 1, 6, 1) \cdot p(i). \]關(guān)于 \(f\) 的方程組中的第四個(gè)方程的含義為:如果抽中了 UP 五星角色,則清空保底的累計(jì)抽數(shù),重新進(jìn)入小保底階段,且抽出的 UP 角色數(shù)增加 \(1\)。\(f\) 仍然可以迭代計(jì)算,只需要分別從小到大枚舉 \(i, j, k\)。 仍然沿用上面部分的代碼,做一些基礎(chǔ)修改后,核心計(jì)算部分如下: MAX_PULLS = 180 * 7 PITY = 90 f = np.zeros((MAX_PULLS, PITY, 7, 2)) result = np.zeros(MAX_PULLS + 1) ### Calculate f[0][0][0][0] = 1 for i in range(0, MAX_PULLS): for j in range(0, min((i + 1, PITY))): result[i + 1] += f[i][j][6][0] * single_rate[j + 1] * 0.5 result[i + 1] += f[i][j][6][1] * single_rate[j + 1] for k in range(0, 7): if i + 1 < MAX_PULLS: if j + 1 < PITY: for x in range(0, 2): f[i + 1][j + 1][k][x] += f[i][j][k][x] * (1 - single_rate[j + 1]) f[i + 1][0][k][1] += f[i][j][k][0] * single_rate[j + 1] * 0.5 if k < 6: f[i + 1][0][k + 1][0] += f[i][j][k][0] * single_rate[j + 1] * 0.5 f[i + 1][0][k + 1][0] += f[i][j][k][1] * single_rate[j + 1]輸出的期望抽數(shù) \(E_3 = 654.121986\)。事實(shí)上,它恰好為 \(E_2 = 93.445998\) 的 \(7\) 倍。\(P(i)\) 本身及其前綴和關(guān)于抽數(shù)的圖象如下:
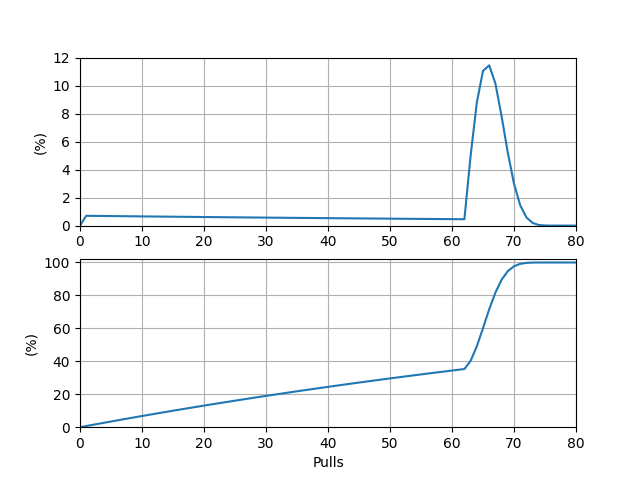
\(P(i)\) 圖象的峰值位于點(diǎn) \((644, 0.00345)\) 處,這表明從零開始抽卡,最有可能在第 \(644\) 抽時(shí)出滿命的目標(biāo) UP 角色,概率約為 \(0.345\%\)。前綴和圖象的 \(50\%\) 對應(yīng)的抽數(shù)在 \(653\) 與 \(654\) 之間,距 \(653\) 更近,這表明中位抽數(shù)約為 \(653\)。 ? 2.3 進(jìn)一步結(jié)果抽取武器與抽取角色總體類似,獲取到的函數(shù) \(p\) 如下: \[p(i) = \begin{cases}0.007, &i < 63,\\ p(i - 1) + 0.07, &63 \leq i < 74, \\ \min\{1, p(i - 1) + 0.035\}, &i \geq 74.\end{cases} \]此外,在抽取 UP 武器時(shí)還需考慮定軌機(jī)制,但這僅是在 \(f\) 中添加一個(gè)參變量的事。例如,在計(jì)算抽滿精目標(biāo)五星 UP 武器的相應(yīng)概率時(shí),我們將會(huì)設(shè) \(f(i, j, k, l, x)\) 表示在前 \(i\) 抽沒有抽滿目標(biāo) UP 武器,保底情況為 \(x\)(\(0\) 為小保底,\(1\) 為大保底),保底累計(jì)抽數(shù)為 \(j\),定軌數(shù)值為 \(k\),且已經(jīng)獲得了 \(l\) 把目標(biāo) UP 武器的概率。各個(gè)抽取目的下的具體分析略,這里僅給出最終結(jié)果。 ? 2.3.1 抽五星(忽略 UP 與否)武器抽取一把五星武器(忽略 UP 與否)的期望抽數(shù) \(E_4 = 53.250420\)。\(P(i)\) 本身及其前綴和關(guān)于抽數(shù)的圖象如下:
\(P(i)\) 圖象的峰值位于點(diǎn) \((66, 0.114)\) 處。前綴和圖象的 \(50\%\) 對應(yīng)的抽數(shù)在 \(64\) 與 \(65\) 之間,距 \(64\) 更近。 ? 2.3.2 抽五星 UP 武器抽取一把目標(biāo)五星 UP 武器的期望抽數(shù) \(E_5 = 105.668802\)。\(P(i)\) 本身及其前綴和關(guān)于抽數(shù)的圖象如下:
\(P(i)\) 圖象的峰值位于點(diǎn) \((66, 0.0445)\) 處。前綴和圖象的 \(50\%\) 對應(yīng)的抽數(shù)在 \(98\) 與 \(99\) 之間,距 \(98\) 更近。 ? 2.3.3 抽滿精五星 UP 武器抽取滿精目標(biāo)五星 UP 武器的期望抽數(shù) \(E_6 = 528.344012\)。\(P(i)\) 本身及其前綴和關(guān)于抽數(shù)的圖象如下:
\(P(i)\) 圖象的峰值位于點(diǎn) \((531, 0.00336)\) 處。前綴和圖象的 \(50\%\) 對應(yīng)的抽數(shù)在 \(526\) 與 \(527\) 之間,距 \(526\) 更近。 ? 3 模型分析我們的分析均基于上面計(jì)算得到的數(shù)據(jù)與圖象。 ? 3.1 模型優(yōu)點(diǎn)當(dāng)我們觀察 2.2.3 與 2.3.3 部分求得的兩幅 \(P(i)\) 圖象時(shí),也許會(huì)驚異于其近似為正態(tài)分布,或者它們的前綴和圖象足夠光滑美觀。正態(tài)分布通常是我們最能接受的概率分布,尤其是在抽取滿命角色或滿精武器這樣投入周期較長或資源較大的抽卡模型中——當(dāng)我們付出較多時(shí),我們希望回報(bào)等級至少在分布上足夠均衡,這樣我們既能對獲取高等級回報(bào)抱以足夠的期待,同時(shí)又不必太擔(dān)心自己的收獲很差。在面對部分抽卡評價(jià)系統(tǒng)給出的“非酋”等級的評估時(shí),許多玩家甚至僅僅希望變得更“平庸”一些,即接近中間水平。正態(tài)分布模型給予了他們歸宿。 站在游戲策劃的角度,單抽出金(這里指角色池)的抽數(shù)集中在 \(77\) 抽左右這一設(shè)計(jì)也較為巧妙。一方面,它離 \(0\) 抽有足夠的距離,這保證了絕大多數(shù)人在為角色買單時(shí)都需要付出足夠的代價(jià),更直白地說,它保證了游戲的收入;另一方面,它在從零開始的第八個(gè)“十連”末尾,卻又沒有進(jìn)入到真正吃滿保底需要的第九個(gè)“十連”中,這會(huì)使大部分玩家慶幸于自己沒有“臉黑”,從而產(chǎn)生“提前出貨”的主觀滿足。 ? 3.2 模型缺陷盡管在上一部分模型優(yōu)點(diǎn)中,我們對抽取滿命角色或滿精武器的概率分布給予了一定的肯定,但不要忘記了,原神作為一款免費(fèi)游戲,其中的大部分玩家并沒有抽取滿命角色與滿精武器的精力與資本。我們還應(yīng)將視線放回到抽取單個(gè)五星角色/武器的概率分布上。可惜的是,我們看到的結(jié)果并不盡如人意。 以抽取單個(gè)五星角色(忽略 UP 與否)為例。盡管出貨的中位抽數(shù)和最大概率抽數(shù)在 \(76\) 附近,相應(yīng)圖象表明分布也確實(shí)較為集中,但期望抽數(shù)卻僅有 \(62.3\)。這說明在 \(74\) 抽(依據(jù)函數(shù) \(p\),出貨概率開始提升的時(shí)候)之前出貨的概率雖然較小,卻不可忽略。事實(shí)上,前綴和給出在前 \(74\) 抽出貨的概率已經(jīng)超過了 \(1/3\)!這會(huì)導(dǎo)致的最直接后果便是大量的幸存者偏差現(xiàn)象——不小的提前出貨的概率使一部分人嘗到了甜頭,這種喜悅蔓延到更大部分保守出貨的人面前時(shí),他們就會(huì)在默默承受痛苦之余感慨一句“吃檸檬,陌生人!”,并對整個(gè)抽卡系統(tǒng)充滿抱怨。 武器池設(shè)計(jì)的不平衡更為明顯。從抽取五星角色到抽取五星 UP 角色,最大概率抽數(shù) \(77\) 保持不變,中位抽數(shù)僅僅從 \(75\) 提升到了 \(80\),并且它們都在 \(77\) 的附近。但同樣是保持一致的最大概率抽數(shù),從抽取五星武器到抽取目標(biāo)五星 UP 武器,中位抽數(shù)從 \(64\) 直接提升為了 \(98\),后者已經(jīng)遠(yuǎn)遠(yuǎn)大于了最大概率抽數(shù) \(66\)。中位數(shù)與眾數(shù)的較大差距表明了模型設(shè)計(jì)必然存在著不合理之處,同時(shí),這一比較也表明引入定軌機(jī)制僅僅防止了如某經(jīng)典“天空之卷”事件的小概率情形的發(fā)生,武器池更深層次的隱患仍沒有被清除。 ? 4 其他說明本文用于數(shù)據(jù)計(jì)算與圖象生成的所有代碼均可在 https://cloud.tsinghua.edu.cn/d/e5ec914057084c56869c/ 查看。 本文中用到的計(jì)算概率函數(shù) \(f\) 的思想實(shí)際名為“動(dòng)態(tài)規(guī)劃”,但由于本文力求科普,所涉及的轉(zhuǎn)移也并不復(fù)雜,因此在前面隱匿了這一名稱,并且將狀態(tài)轉(zhuǎn)移方程族簡單地稱為“方程組”。實(shí)際上,每個(gè)等式的含義已經(jīng)由等式本身直接體現(xiàn),但在必要處我們?nèi)赃M(jìn)行了解釋說明。 |
【本文地址】
| 今日新聞 |
| 推薦新聞 |
| 專題文章 |